Mathématiques,
nombres complexes.
Concours Geipi Polytech .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Epreuve 2016.
Le plan complexe est muni d’un repère orthonormé direct (O; u, v).
Soient A, B et C les points d’affixes respectives zA = 1, zB
= 1 + i et zC = i.
Soit x un réel appartenant à ]0, 1[.
On nomme :
M le point du segment [AB] d’affixe zM = 1 + xi ;
N le point du segment [BC] d’affixe zN = x + i.
Posons Z =zN / zM.
Partie A.
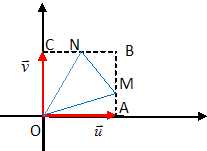
A-1- Sur la figure,
le point M a été placé pour une certaine valeur du réel x.
Tracer le carré OABC et le triangle OMN.
A-2- Exprimer, en
fonction de x, les modules |zM| et |zN|.
|zM| = (1+x2)½ ; |zN| = (1+x2)½.
A-3- Le triangle OMN est isocèle.
Donner son sommet principal. Justifier la réponse.
OM = |zM| ; ON =
|zN| ; le
triangle OMN est isocèle en O.
A-4-a- Montrer que la droite (OB)
est perpendiculaire à la droite (MN).
Coefficient directeur de la droite (OB) : +1.
Coefficient directeur de la droite (MN) : (yM-yN)
/ (xM-xN) = (x-1) / (1-x) = -1.
Le produit de ces deux coefficients directeurs étant égal à -1, les
droites (OB) et (MN) sont perpendiculaires.
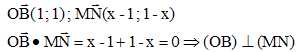
A-4-b- En déduire
que la droite (OB) est la bissectrice de l’angle MON.
Dans le triangle OMN, isocèle en O, la hauteur issue du sommet O est
également bissetrice de l'angle MON.
A-5- Justifier que
|Z| = 1.
|Z| = |zM| /
|zN| =(1+x2)½
/ (1+x2)½ =1.
A-6- Montrer que la
forme algébrique de Z est : Z =[2x+i(1-x2)] / (1+x2).
Z =(x+i) /(1+xi) = (1-xi)(x+i) / (1+x2).
Z = (x + i - ix2+ x) / (1+x2).
Z = [2x + i(1-x2)] / (1+x2).
A-7- Im(Z) désigne la partie
imaginaire de Z. Montrer que Im(Z) > 0.
Im(Z) =(1-x2)
/ (1+x2) avec x appartenant à ]0 ; +1[.
Im(Z) >0.
Partie B.
Dans cette partie x = 2 − 3½.
B-1- Donner la
valeur exacte de 1 + x2.
1+(2-3½)2 = 1+(4 -4 *3½ +3) = 8-4*3½.
B-2-a- Re(Z)
désigne la partie réelle de Z. Montrer que Re(Z) =½.
Re(Z) = 2x / (1+x2) = 2( 2 − 3½)
/ ( 8-4*3½)
= ½..
B-2-b- On nomme q un argument de Z.
En déduire, en utilisant certains résultats de la Partie A, la valeur
exacte de q.
tan q = Im(Z) /
Re(Z) = 2(1-x2)
/ (1+x2).
1-x2 = 1-(2-3½)2
= 1-(4 -4 *3½ +3) = -6+4*3½.
tan q =(-6+4*3½) / (4-2*3½).
tan
q =(-6+4*3½) (4+2*3½)/ (16-12)
= (-24-12 *3½ +16*3½ +24) / 4 = 3½ ; q = 60° ou ( p / 3).
B-3-a- En utilisant la
question A-4-b-, donner une mesure de l’angle MOB.
L'angle MON mesure
p / 3
radian ; OB est la bissectrice de cet angle ;
l'angle MOB mesure p / 6 radian.
B-3-b- Montrer que l'angle AOM
mesure p / 12 radian.
La droite (OB) est axe de symétrie de la figure.
La somme des mesures des angles AOM et MOB est égale à p/4 radian.
p/4 - p/6 = p/12 radian.
B-4-a- Justifier que 1 + x2
= (6½-2½)2.
.1
+ x2 = 8-4*3½ =
(a-b)2 =a2 +b2-2ab.
Par identification : a2
+b2 = 8 et 2ab = 4*3½
; soit a = 2*3½ / b.
12 / b2 + b2 = 8
; b4-8b2+12 = 0 ; solutions b2 = 2 ; b2
=6.
par suite a2 = 6 ou a2 = 2 ; a =±2½ et
b = ±6½.
Si a = 2½, alors b = 6½ ; si
a = -2½, alors b = -6½.
B-4-b-
En déduire la valeur exacte de |zM|.
|zM| = 1 + x2 = (6½-2½)2.
B-5- Ecrire la forme trigonométrique
de zM.
zM = (6½-2½) [cos (p/12)
+ i sin (p/12)]
B-6- On en déduit que cos (p/12) = a / (6½-2½) et sin (p/12) = b / (6½-2½),
où a et b sont des réeels.
Donner les valeurs exactes de a et b.
zM = (6½-2½) [cos (p/12)
+ i sin (p/12)]
=1+ix.
Par identification cos (p/12)
= 1 / (6½-2½) ;
et sin (p/12)
= x /(6½-2½) = (
2 − 3½ ) /(6½-2½).
a = 1 et b =
2 − 3½ .
|
| .
. |
|
|
Epreuve 2015.
Le plan complexe est muni d’un repère orthonormé (O ; u , v).
On considère les points A, B d’affixes respectives zA = 1 et
zB = 0,5(-1 + 3½ i).
Soit C le symétrique de B par rapport à l’axe des abscisses.
Partie A.
A-1- Tracer le triangle ABC sur la
figure.
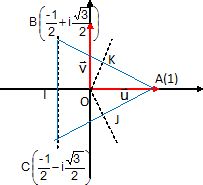
A-2- Donner l’affixe zC
du point C
zC = 0,5(-1 - 3½ i).
A-3-a- Calculer le module |zB
− zA|. Détailler le calcul.
zB − zA = 0,5(-3
+ 3½ i) ;
|zB − zA| =0,5 [(-3)2
+3]½ = 0,5 *12½ =3½.
A-3-b- Donner les modules |zC
− zA| et |zC − zB|.
zC − zA = 0,5(-3
- 3½ i) ;
|zC − zA| =0,5 [(-3)2
+3]½ = 0,5 *12½ =3½.
zC − zB = (-
3½ i) ;
|zC − zB| =(3)½
= 3½.
A-3-c- En déduire la nature du
triangle ABC.
Le triangle ABC est équilatéral.
Partie B.
On considère les points suivants :
I : projeté orthogonal du point O sur la droite (BC),
J : projeté orthogonal du point O sur la droite (AC),
K : projeté orthogonal du point O sur la droite (AB).
On désigne par zI , zJ et zK leurs
affixes respectives.
B-1- Placer les
points I, J et K sur la figure.
B-2-a- Justifier
que J est le milieu du segment [AC].
OA= 1 ; OC = 0,5 [(-1)2 +(-3½)2]½
= 1.
Le triangle OAC est isocèle en O et OJ est la hauteur issue de O, c'est
aussi la médiatrice du segment [AC].
B-2-b-
Calculer alors l’affixe zJ de J. Donner son module |zJ|.
(xA +xC) / 2 = (1
-0,5) / 2 =0,25 ; (yA +yC) / 2 = (0
-0,5*3½) / 2 =-3½ /4.
zJ = 0,25(1-3½ i) ; |zJ| =0,25[12+(-3½)2]=0,5.
B-2-c- Donner les affixes zI
et zK ainsi que leur module |zI | et |zK|.
K est le symétrique de J par rapport à l'axe des abscisses.
zK = 0,25(1+3½ i) ; |zK| =0,5.
zI = -0,5 ; |zI| =0,5.
B-3- En déduire la valeur de la
somme des distances : LO = OI + OJ + OK. Justifier la
réponse.
LO = |zJ| +|zI| + |zK| = 1,5.
Partie C
Soit M un point quelconque situé à l’intérieur du triangle ABC.
On considère les points suivants :
E : projeté orthogonal de M sur la droite (BC),
F : projeté orthogonal de M sur la droite (AC),
G : projetée orthogonal de M sur la droite (AB).
On note A1, A2, A3 et A les aires
respectives des triangles MBC, MAC, MAB et ABC.
On pose LM = ME + MF + MG.
C-1- Avec le point
M dèjà placé sur la figure, placer les points E, F et G.
C-2-a- Exprimer A1
en fonction de la distance ME.
C-2-b- Ecrire une
relation liant A1, A2, A3 et A.
C-2-c- Déduire des
questions précédentes que : A =3½ LM /2.
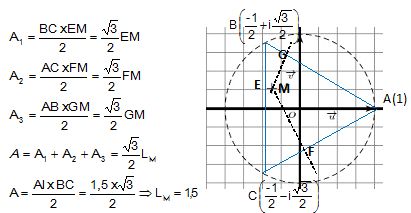
C-3- L’égalité
précédente montre que la valeur de LM ne dépend pas de la
position du point M à l’intérieur du triangle ABC. Donner la valeur de LM.
Justifier la réponse.
Par identification des deux expressions de A ci-dessus : LM
=1,5.
|
|
|
|
2013.
On se place dans le plan complexe rapporté au repère (O; u , v )
orthonormé, direct.
On considère la fonction polynomiale P définie par :
pour tout complexe zappartenant à C, P(z) = z4 − 6z3
+ 14z2 − 6z + 13 .
1-a- Calculer P(i)
et P(−i).
P(i) = i4 − 6i3 + 14i2 − 6i + 13
= 1+6i-14-6i+13=0
P(-i) = (-i)4 − 6(-i)3 + 14(-i)2 −
6(-i) + 13 = 1-6i-14+6i+13=0
1-b- Pour tout
complexe z, on a l’égalité : P(z) = (z2 + 1)Q(z)
où Q(z) s’écrit sous la forme : Q(z) = z2 + cz + d.
Donner les valeurs des réels c et d.
P(z) = (z2 + 1)(z2 + cz + d)=z4+cz3+dz2+z2
+ cz + d.
On identifie : c = -6 et d = 13.
1-c- Déterminer
l’ensemble S1 des solutions, dans C, de l’équation Q(z) = 0.
Justifier le résultat.
z2 -6z +13=0.
Discriminant D' = 9-13 = -4
= 4 i2.
Solution z1 = 3+2i et z2 = 3-2i.
1-d- En déduire
l’ensemble S2 des solutions, dans C, de l’´equation P(z) = 0.
z2+1 = 0 conduit à z = ±i, d'où S2 ={3-2i ; -i ;
+i ; 3+2i }
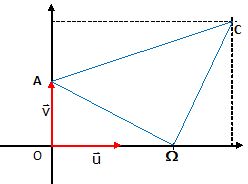
2- Placer sur la
figure les points A, C et W
d’affixes respectives :
zA = i, zC = 3 + 2i, zW= 2.
3-a- On note Z1,
Z2 et Z3 les affixes respectives des vecteurs 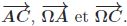
Donner les valeurs de Z1, Z2 et Z3.
Z1 = 3+2i-i = 3+i ; Z2 = i-2 ; Z3 =
3+2i-2 = 1+2i.
3-b- Donner alors
les modules |Z1|, |Z2|, |Z3| de Z1,
Z2, Z3.
|Z1| = [32+12]½=10½
; |Z2| = [(-2)2+12]½=5½
; |Z3| = [22+12]½=5½
;
3-c- Déterminer
alors les valeurs exactes des distances AC, WA et WC. Justifier les réponses.
AC = |zC-zA| =
|Z1| =10½ ; WA=|zA -zW| =
|Z2| =5½ ;
WC=|zC -zW
=
|Z3| =5½ .
3-d- Déterminer une
mesure, en radians, de l’angle géométrique WAC. Justifier.
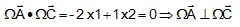
L'angle géométrique WAC
mesure ½p radian.
3-e- Quelle est la
nature précise du triangle AWC
?
AC2 = WA2
+WC2,
le triangle WAC
est rectangle en W.
4- On considère les points B et D
d’affixes respectives :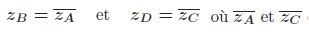 désignent
respectivement les complexes conjugués de zA et zC. désignent
respectivement les complexes conjugués de zA et zC.
4-a- Placer les
points B et D sur la figure .
4-b- Justifier que
les points A, B, C et D sont sur un même cercle. Préciser son centre et
son rayon r.
4-c- Tracer ce
cercle sur la figure.
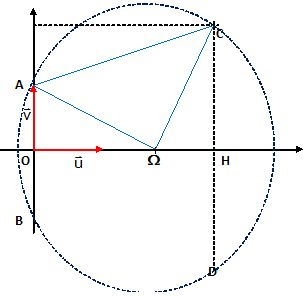
WA = WC = 5½ ; WB =|zB -zW| =|zA
-zW|=
|Z2| =5½ ; WD =|zD -zW| = |zC
-zW| =|Z3| =5½
;
le centre du cercle est le point W et son réyon vaut r = 5½.
III-5-
Donner l’aire A, en unités d’aires, du trapèze ABDC.
AB = |zB-zA|=| -i -i | =2. CD
= |zD-zC|=| -2i -2i | =4. OH = 3.
A = ½(AB +CD) x OH = 1,5 x(4+2) = 9 unités d'aire.
|
|