Statistiques,
probabilités, pourcentage : bac St2S 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
L’évolution
de l’endettement d’une entreprise est donnée par le tableau suivant,
extrait d’une feuille de calcul.
|
A |
B |
C |
D |
E |
F |
G |
| 1 |
Année |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
| 2 |
Endettements (
milliers d'euros) |
400 |
410 |
|
|
|
|
| 3 |
Pourcentage
d'évolution entre
2 années consécutives |
|
|
|
|
|
|
Le pourcentage
d’augmentation de l’endettement de l’entreprise entre les années 2011
et 2012 est :
a) 0,25 % ; b) 2,5 % ;c) 10,25 % ; d)0,025 %.
(410-400) / 400 *100 = 2,5 %.
À partir de l’année 2012, on admet que l’endettement de l’entreprise
diminuera chaque année de 5%.
La
formule à saisir dans la cellule D2, qui recopiée vers la droite,
permettra d’afficher les valeurs en milliers d’euros de l’endettement
de l’entreprise pendant les années qui suivent 2012 est :
a) =410*0,25 ; b) =C2*0,05 ; c) =C2*0,95 ; d) =$C$2*0,95.
=C2*0,95.
On désigne par n un entier naturel. On note un
l’endettement de l’année 2012+n, ainsi u0 = 410. L’endettement de
l’entreprise en milliers d’euros pendant l’année 2020 est :
a) u8 = 410×0,958 ; b) u8 = 410×0,959
; c). u9 = 410×0,958 ; d) u9 = 410×0,959.
En 2013 : u1 = 0,95 u0 ; en 2014 : u2 = 0,95 u1
=0,95*0,95 u0 = 0,952u0 ; en 2012 +n :
un = 0,95n u0.
En
2020, n =8 : u8 = 410×0,958.
On
cherche à partir de quelle année l’endettement de l’entreprise aura
diminué de moitié. Pour cela l’inéquation à résoudre s’écrit 410×0,95n
<= 205, où n désigne un entier naturel. Les solutions de
cette inéquation sont les entiers n tels que : a) n<=log 0,5
/ log 0,95 ; b) n>= log0,5 / log 0,95 ; c) n>=log (0,5/0,95) ; d)
n<=log(0,5/0,95).
2×0,95n
<= 1 ; 0,95n <=0,5 ; n
log 0,95 <= log 0,5 ; n(-log 0,95) >-log0,5 ; n >= log 0,5
/log 0,95.
Dans
le tableau les cellules C3 à G3 sont en pourcentages. La formule à
saisir dans la cellule C3, qui recopiée vers la droite, permet
d’afficher le pourcentage d’évolution de l’endettement de l’entreprise
entre deux années consécutives est : a. =($C2-$B2)/$B2 ; b. =C2-B2/B2 ;
c. =C2/B2 ;d. =(C2-B2)/B2.
|
|
|
Fin
2010, 1 200 000 personnes âgées dépendantes ont bénéficié de
l’Allocation Personnalisée d’Autonomie (APA), soit à domicile, soit en
établissement. Ces personnes sont classées dans quatre Groupes
Iso-Ressources (GIR) en fonction des différents stades de pertes
d’autonomie. Les résultats, exprimés en milliers de personnes, d’une
enquête réalisée en 2010 auprès des conseilsgénéraux ont permis de
construire le tableau suivant.
Les nombres sont exprimés en
milliers de personnes.
|
à domicile |
en établissement |
total |
| en GIR1 |
19 |
86 |
105 |
| en GIR2 |
131 |
191 |
322 |
| en GIR3 |
159 |
79 |
238 |
| en GIR4 |
425 |
110 |
535 |
| Total |
734 |
466 |
1200 |
Justifier, par un
calcul approprié, chacune des informations suivantes dans lesquelles
les résultats ont été arrondis à l’unité.
Le pourcentage des personnes de l’étude qui vivent à domicile est égal
à 61%.
734*100 / 1200 =61 %.
3% des personnes de l’étude vivant à domicile sont classées en
GIR1.
19 / 734*100=2,58 ~3 %.
Pour
chacune des questions suivantes, on donnera les résultats sous forme
décimale, arrondie au centième. On choisit au hasard le dossier d’une
personne agée dépendante bénéficiant de l’APA. On considère les
évènements suivants :
G : « Le dossier est celui d’une personne
classée en GIR1 ». E : « Le dossier est celui d’une personne vivant en
établissement ». Calculer la
probabilité des évènements G et E.
p(G) =105/1200 =0,0875 ~0,088 ; p(E) =466/1200 =0,388 ~0,39.
Définir
par une phrase chacun des évènements suivants puis calculer leur
probabilité.
Le dossier est celui d’une personne classée en GIR1 et vivant en
établissement :
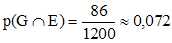
Le dossier est celui d’une personne classée en GIR1 ou vivant en
établissement.
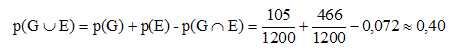
Sachant que le dossier choisi est celui d’une personne classée en GIR4,
calculer
la probabilité que cette personne vive à domicile.
425 / 535 =0,794 ~0,79.
Calculer
PE (G). 0,072 /
p(E) =0,072 / (466/1200) ~0,19.
|
.
|
|
Le
service de l’eau d’une ville a été privatisé en 1990, puis géré par la
commune à partir de 1996. Le tableau ci-dessous, extrait d’une feuille
de calcul, donne l’évolution du prix del’eau de cette ville, en euros
pour 120 m 3, entre les années 1990 et 1996.
|
A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
année |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
| 2 |
prix de 120 m3
(€) |
185 |
177 |
189 |
208 |
216 |
222 |
228 |
| 3 |
taux d'évolution (ù)
entre 2 années consécutives |
|
|
|
|
|
|
|
Calculer
le taux d’évolution du prix de 120 m3 d’eau entre 1990 et
1991.
(177-185) / 185 *100 = -4,3 %.
Quelle
formule doit-on rentrer dans la cellule D3, qui recopiée vers la
droite, donne le pourcentage d’évolution du prix de 120m3 d’eau entre deux
années consécutives ?
=(D2-C2) / C2 *100.
On admet que, si le service de l’eau était resté privatisé, le prix de
120 m3 aurait augmenté de 2,5% par an à partir de l’année
1996.
On note alors un le prix de 120 m3 d’eau pour l’année
(1996+n) où n est un entier naturel. On a alors u0
= 228.
Justifier
que la suite (un) est une suite
géométrique dont on précisera la raison.
u1 =1,025 u0 ; u2 = 1,025 u1
= 1,025*1,025u0 = 1,0252u0.....un
=1,025nu0.
Quel
aurait été le prix de 120 m3 d’eau en 2012 si le
service était resté privatisé ?
n =2012-1996=16 ; u16 =1,02516*228=338 €.
À
partir de quelle année, le prix de 120 m3 d’eau aurait-il
dépassé 300 € ?
1,025nu0 >300 ; 228 *1,025n>300
; 1,025n>1,316 ; n log 1,025 > log 1,316 ; n
> log 1,316 / log 1,025 ; n >11,14.
A partir de 1996+12 = 2008, le prix de ce volume d'eau sera supérieur à
300 €.
La ville gère le service de
l’eau depuis 1996. Le tableau ci-dessous donne l’évolution du prix de
120 m3 d’eau depuis 1998.
| année |
1998 |
2000 |
2002 |
2004 |
2006 |
2008 |
2010 |
2012 |
| rang de l'année xi |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
| prix de 120 m3
d'eau (€) yi |
191 |
202 |
198 |
202 |
204 |
208 |
215 |
220 |
Représenter le nuage
de points de coordonnées dans un repère orthogonal. Déterminer les
coordonnées du point moyen G de ce nuage de points. Placer le point
moyen G dans le repère.
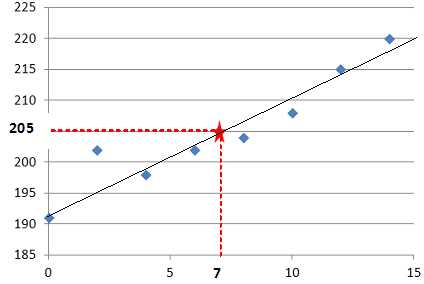
.
On
admet que la droite (¢) d’équation y = 1,8x+192,4 réalise un ajustement
affine du nuage de points. Cet ajustement est fiable jusqu’en 2020.
Vérifier
que le point moyen G appartient à la droite. Tracer la droite
dans le repère précédent.
205=1,8*7+192,4 ; cette égalité
étant vérifiée, G appartient à cette droite.
En
tenant compte de cet ajustement affine, déterminer le prix de 120 m3 d’eau que l’on peut
prévoir pour l’année 2020.
En 2020, x = 22 et y = 1,8*22+192,4 =232 €.
..
|
|
Une
enquête a été menée auprès de 1 700 habitants de diverses régions
françaises consommant de l’eau du robinet ou de l’eau en bouteille. Les
résultats de l’enquête sont répartis par région dans le tableau
ci-dessous :
| Région |
Nombre de personnes
consommant l'eau du robinet |
Nombre de personnes
consommant l'eau en bouteille |
Total |
| Paris |
557 |
274 |
831 |
| Nord |
224 |
243 |
467 |
| Sud ouest |
309 |
93 |
402 |
| Total |
1090 |
610 |
1700 |
On
considère les évènements suivants : N : « La personne interrogée habite
dans la région nord. » R : « La personne interrogée consomme de l’eau
du robinet. »
Pour chacune des questions suivantes, on donnera les résultats sous
forme décimale, arrondie au centième.
On choisit au hasard une personne parmi toutes les personnes
interrogées.
Calculer
les probabilités suivantes.
p(R) =1090 / 1700 =0,64
Probabilité qu'une personne interrogée ne consomme pas d'eau du robinet
:1-0,64 =0,36 ou bien 610/1700 =0,36.
Probabilité qu'une personne habite la région nord et consomme de l'eau
du robinet : 224 / 1700 =0,13.
Probabilité qu'une personne interrogée habite dans la région nord ou
consomme de l’eau du robinet.
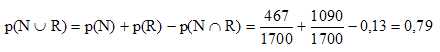
On veut comparer le type de consommation d’eau suivant les régions :
Déterminer
la probabilité qu’une personne interrogée consomme l’eau du robinet
sachant qu’elle habite la région nord.
224 / 467=0,48.
Dans
quelle région faudrait-il se placer pour que la probabilité qu’une
personne interrogée consomme l’eau du robinet soit la plus élevée
?
Paris : 557 / 831 =0,67 ; sud ouest
: 309 / 402 = 0,77.
|
|
|
|