Suite
géométrique, suite arithmétique,
bac Sti2d.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
L’algorithme
ci-dessous permet de calculer les termes successifs d’une suite que
l’on appellera (un).
Entrée : Saisir la valeur de l’entier naturel n
Traitement : Affecter 2 à la variable u
Pour i variant de 1 à n
Affecter 1,5u à u
Fin de Pour
Sortie : Afficher u
Quelles
valeurs affiche cet algorithme lorsque l’on saisit n = 1, puis n = 2 et
enfin n = 3 ?
u1 = 1,5*2 = 3 ; u2
=3*1,5 = 4,5 ; u3 = 1,5*4,5 =6,75
On considère la suite (un) définie par u0 = 2
et, pour tout entier naturel n, un+1 = 1,5un
.
Quelle
est la nature de la suite (un) ?
Préciser ses éléments caractéristiques.
Il s'agit d'une suite géométrique de raison 1,5 et de premier terme 2
Pour
tout entier naturel n, donner l’expression du terme un en
fonction de n.
u1 = 1,5 u0 ; u2
= 1,5 u1
=1,5* 1,5
u0 = 1,52u0
=1,52*2
; un = 1,5n *2.
On
considère la suite (Sn)
définie pour tout entier naturel n par :
Sn =u0+u1+u2+.....un.
Calculer
les valeurs des termes S0, S1
et S2.
S0
=u0
= 2 ; S1 =u0 +u1
=2+3 =5 ; S2 =u0
+u1
+u2 =2+3 +4,5 =9,5.
Quelles
modifications doit-on faire à l’algorithme précédent pour qu’il affiche
la valeur du terme Sn pour un n donné ?
Entrée
: Saisir la valeur de l’entier
naturel n
Traitement : Affecter 2 à la variable u
Affecter 2 à la variable S
Pour i variant de 1 à n
Affecter 1,5u à u
S = S+u
Fin de Pour
Sortie : Afficher S
Calculer
le terme Sn en
fonction de l’entier naturel n.
Sn
= u0+u1+u2+.....un
= u0(1-qn+1) / (1-q) =2((1-1,5n+1)
/ (1-1,5)= 4(1,5n+1-1).
|
| .
. |
.
|
|
On considère la suite
numérique (un) définie par : u0 = 8 et, pour tout
entier naturel n, un+1 = 0,4un +3.
Calculer
u1 et u2.
u1 =0,4 u0+3 =0,4*8+3 =6,2 ; u2 =0,4 u1+3
=0,4*6,2+3 =5,48.
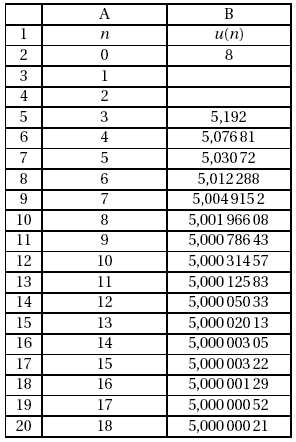
On
utilise un tableur pour calculer les premiers termes de cette suite.
Une copie d’écran sur laquelle les termes u1 et u2
ont été effacés est donnée.
Quelle
formule a-t-on pu saisir dans la cellule B3 de la feuille de calcul
afin d’obtenir les premiers termes de cette suite par recopie vers le
bas ?
=0,4*B2+3
En
utilisant cette copie d’écran, que peut-on conjecturer sur la limite de
la suite (un) ?
La suite tend vers 5.
On considère l’algorithme suivant :
Les variables sont l’entier naturel N et le réel U.
Initialisation : Affecter à N la valeur 0
Affecter à U la valeur 8
Traitement : TANT QUE U−5 > 0,01
Affecter à N la valeur N + 1
Affecter à U la valeur 0,4U+3
Fin TANT QUE
Sortie : Afficher N
Par
rapport à la suite (un), quelle est la
signification de l’entier N affiché ?
N est le plus petit entier à partir duquel un-5 devient
inférieur à 0,01.
On considère la suite (vn) définie pour tout entier naturel
n, par vn = un −5. On admet que la suite (vn)
est géométrique de premier terme v0 = 3 et de raison 0,4.
Exprimer
vn en fonction de n.
v1 = 0,4 v0 =0,4(u0-5) ; v2 = 0,4 v1
=0,42v0 ; vn = 0,4nv0
=0,4n*0,3.
Déterminer la limite
de la suite (vn).
La limite de la suite (un) est 5 ; la limite de la
suite (un)-5 est zéro.
La raison est comprise entre -1 et 1 la limite de la suite (vn)
est nulle.
Le
résultat précédent permet-il de valider la conjecture faite à la
question 3 ? Pourquoi ?
un =vn+5 ; lim un = 5 + lim vn
= 5+0 = 5.
|
Depuis
2000, l’Union Européenne cherche à diminuer les émissions de polluants
(hydrocarbures et oxydes d’azote) sur les moteurs diesel des véhicules
roulants. En 2000, la norme tolérée était fixée à 635 milligrammes par
kilomètre en conduite normalisée. L’objectif de l’Union Européenne est
d’atteindre une émission de polluants inférieure à 100 milligrammes par
kilomètre.
La norme est réactualisée chaque année à la baisse et depuis 2000, sa
baisse est de 11,7% par an.
Justifier
que la norme tolérée était d’environ 561 milligrammes par kilomètre en
2001.
635(1-0,117) =561 mg / km.
Un véhicule émettait 500 milligrammes par kilomètre en 2002. Indiquer, en
justifiant, s’il respectait ou non la norme tolérée cette année là.
Norme en 2002 : 561(1-0,117)
=495 mg / km. Le véhicule respecte la norme 2002.
Dans
le cadre d’une recherche, Louise veut déterminer à partir de quelle
année l’Union Européenne atteindra son objectif. Louise a amorcé
l’algorithme suivant :
Variables
n : un nombre entier naturel
p : un nombre réel
Initialisation
Affecter à n la valeur 0
Affecter à p la valeur 635
Traitement
Tant que . . . . . .
Affecter à n la valeur n +1
Affecter à p la valeur 0,883×p
Fin Tant que
Sortie
Afficher . . . . . .
Expliquer
l’instruction « Affecter à p la valeur 0,883×p ».
p prend une nouvelle valeur ; sa valeur précédente est multipliée par
0,883.
Deux lignes de l’algorithme comportent des pointillés. Recopier ces lignes
et les compléter afin de permettre à Louise de déterminer l’année
recherchée.
Tant que p >100 ; Afficher 2000+n.
Pour tout entier naturel n, on note un la norme tolérée,
exprimée en milligrammes l’année (2000+n). On a ainsi u0 =
635.
Établir
que la suite (un) est une suite
géométrique dont on précisera la raison. Pour tout entier
naturel n, exprimer un en fonction de n.
u1
= 0,883 u0 ; u2 = 0,883 u1 = 0,8832
u0..... un = 0,883n u0.
Déterminer
à partir de quelle année l’Union Européenne atteindra son objectif.
0,883n u0< 100 ; n log 0,883 +log u0
<log 100 ; -0,054 n +2,803 < 2 ; 0,054n < -0,803 ; n >
0,803/0,054 ; n >14,8.
En 2015 la norme "inférieur à100 mg /km " sera atteinte.
|
.
|