Nombres
complexes,
bac.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Dans
le plan complexe muni d'un repère orthonormé direct, on appelle f
l’application qui à tout point M d’affixe z différente de −1, fait
correspondre le point M' d’affixe 1/(z+1).
Le but de l’exercice est de déterminer l’image par f de la droite D
d’équation x = −½.
Soient A, B et C les points d’affixes respectives zA = −½, zB
= −½+i et zC = −½-½i.
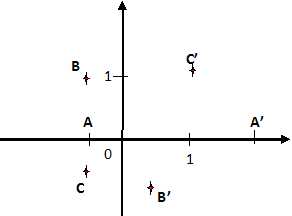
Placer
les trois points A, B et C sur une figure.
Calculer
les affixes des points A' = f(A), B' = f(B) et C' = f(C) et placer les
points A', B'et C' sur la figure.
zA' =1/(-½+1) =1/½ = 2.
zB'
=1/(-½+i+1) =(0,5-i) / ((0,5+i)(0,5-i)) =(0,5-i) / (0,25-i2)=
0,4 -0,8i.
zC'
=1/(-½-½i+1) =(0,5+0,5i) / ((0,5-0,5i)(0,5+0,5i)) =(0,5+0,5i) /
(0,25-0,25i2)= 1+i.
Démontrer que les
points A', B' et C' ne sont pas alignés.
A'(2,0) ; B'(0,4 ; -0,8 ) ; C'(1 ; 1 ).
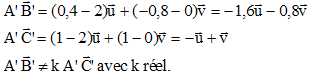
Les points A', B' et C' ne sont donc pas alignés.
|
|
|
Soit g
la transformation du plan qui, à tout point M d’affixe z, fait
correspondre le point M1 d’affixe z + 1.
Déterminer
la nature et les éléments caractéristiques de la transformation g.
Il s'agit d'une translation de vecteur 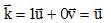
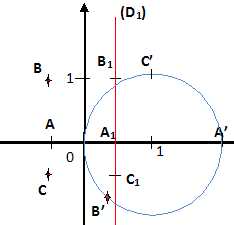
Sans donner d’explication, placer les points A1, B1 et C1, images respectives
par g de A, B et C et tracer la droite D1, image de la droite
D par g.
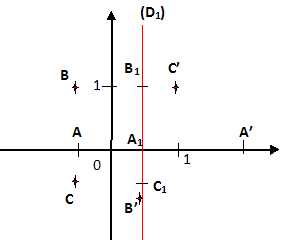
Démontrer
que D1 est l’ensemble des
points M d’affixe z telle que |z − 1| = |z|.
On pose z = a+iß ; |z| =(a2+ß2)½
; |z-1| =((a-1)2+ß2)½
;
|z-1| = |z|
entraîne a = ½.
D1 est l'ensemble des points M tels que zM =½+k
i, k réel.
Il s'agit de la droite d'équation y = 0,5, c'est à dire la droite D1.
|
| .
. |
.
|
|
Soit h
l’application qui, à tout point M d’affixe z non nulle, associe le
point M2 d’affixe 1/z .
Justifier
que h (A1) = A', h (B1) = B' et h (C1)
= C'.
z (A1) =1/0,5 = 2 =z(A') ; z (B1) =1/i =
-i =z(B') ;
z(C1) =1/(0,5-0,5i )=(0,5+0,5i) /((0,5-0,5i )(0,5+0,5i )) =(0,5+0,5i) /(0,25+0,25)=
1+i = z(C').
Démontrer que, pour
tout nombre complexe non nul z, on a : 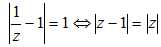
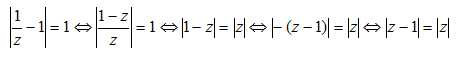
En
déduire que l’image par h le la droite D1 est incluse dans un
cercle C dont on précisera le centre et le rayon. Tracer ce cercle sur
la figure.
On admet que l’image par h de la droite D1 est le cercle C
privé de O.
On considère un point M3 d'affixe z3, autre que
l'origine O, située la droite D1. z(M3)=1/z3
existe.
Déterminer
l’image par l’application f de la droite D.
f(D) =h(g(D)) =h(D1) ; il s'agit du cercle
de rayon 1 et de centre O'(1,0).
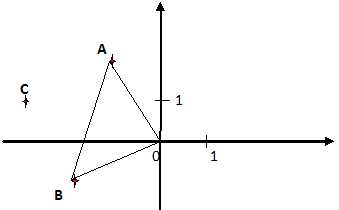
On considère les points A, B et C du plan complexe d'affixes
respectives : a=-1+2i, b=-2-i, c =-3+i.
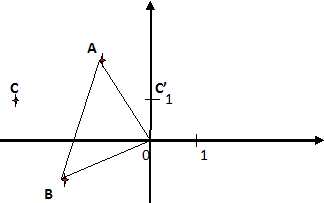
Placer
les points A, B, C sur un graphique.
Calculer
b/a et en déduire la nature du triangle OAB.
b/a = (-2-i) / (-1+2i) = (-2-i)(-1-2i) / ((-1+2i)(-1-2i)) =(2+i+4i+2i2)
/ (1-4i2) = 5i /5 = i
|b/a|=1 ; 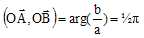 ; OB =OA, le triangle OAB est
isocèle et rectangle. ; OB =OA, le triangle OAB est
isocèle et rectangle.
|
On
considère l'application f qui a out point M d'affixe z ( avec z
diférent de b), associe le point M' d'affixe z' = (z+1-2i) / (z+2+i).
Calculer
l'affixe c' du point C', image de C par f et le placer sur la figure.
z'(C') =(-3+i+1-2i) / (-3+i+2+i) =(-2-i) / (-1+2i) = (2+i) / (1-2i) =(2+i)(1+2i) /
((1+2i)(1-2i) =(2+5i+2i2) / (1-4i2)=5i /5=
i.
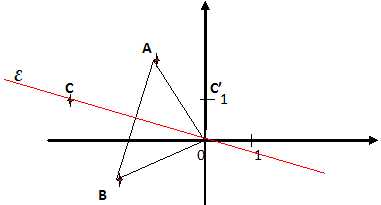
Déterminer
l'ensemble E des
points M d'affixe z ( z différent de b) tels que |z'|=1. Justifier que E contient les points O et
C. Tracer E.
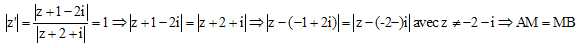
M est différent de B ; M est situé sur la médiatrice du segment [AB].
A(-1 ; 2 ) ; B(-2 ; -1) ; M(x,y) : AM2 = BM2 :
((x+1)2+(y-2)2 =(x+2)2+(y+1)2.
x2+2x+1+y2-4y+4 =x2+4x+4+y2+2y+1.
Equation de cette médiatrice : 6y +2x =0 y=-x/3.
OA = OB : O est
sur la médiatrice de [AB].
Mesure du segment [AC] : [(-2)2 +(-1)2 ]½=5½.
Mesure du segment
[BC] : [(-1)2 +(2)2 ]½=5½.
Ces deux segments ont même mesure : C est sur la médiatrice de [AB].
On
appelle J l'image du point A par rotation r de centre O et d'angle
-90°.
On appelle K l'image du point C par rotation r' de centre O et d'angle
+90°. On note L le milieu de [JK].
Démontrer
que la médiane issue de O du triangle OJK est la hauteur issue de O du
triangle OAC.
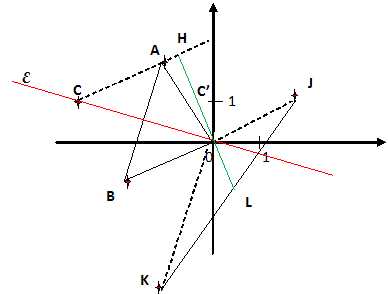
Par rotation de centre O et d'angle -90°, le point J est tel que z(J) =
-i z(A) =-i(-1+2i) =i-2i2 = 2+i ; J(2 ; 1 ).
Par rotation de centre O et d'angle +90°, le
point K est tel que z(K) = +i z(C) = i(-3+i) =-3i+i2 = -1-3i
; K(-1 ; -3 ).
Par suite, les coordonnées du point L, milieu de JK sont : ½(2-1) et
½(1-3) soit L(½ ; -1 ).
A(-1; 2) et C( -3 ;1 ) : 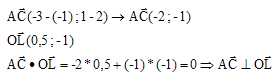
La droite OL étant perpendiculaire à AC, est la hauteur issue de O du
triangle OAC.
|
|