Etude
graphique et numérique de fonction : bac St2S 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pour
traiter un patient, un médecin procède à l’injection intramusculaire
d’une dose d’une substance médicamenteuse au temps t = 0 (t est exprimé
en heures).Le produit actif se
diffuse dans le sang puis est progressivement éliminé.
Le médicament est efficace lorsque la concentration du produit actif
dans le sang est supérieur ou égale à 25mg/L.
La concentration maximale du produit actif dans le sang ne peut pas
dépasser 40 mg/L pour éviter les effets secondaires.
Partie
A : Étude
graphique.
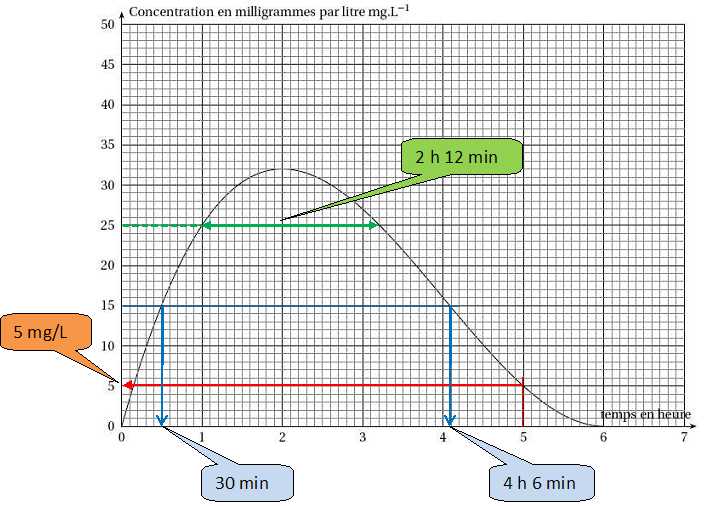
La courbe donnée ci-dessous représente la concentration en mg / L du
produit actif dans le sang du malade en fonction du temps écoulé depuis
l’injection du médicament. À l’aide de cette courbe répondre, avec la
précision que permet le graphique, aux questions suivantes en faisant
apparaître les traits de constructions utiles.
Déterminer la concentration en mg/L du produit actif pout t = 5.
Le médecin a-t-il respecté la dose à ne pas dépasser ? Expliquer.
La valeur maximale de la concentration vaut 32 mg/L, valeur inférieure
à 40 mg/L. le médecin a effectué une injection correcte.
Déterminer les temps en heures et minutes pour lesquelles la quantité
de produit actif est de 15 mg/L.
Quelle est la durée pendant laquelle le médicament est resté efficace ?
Au bout de quelle durée le médicament est-il complètement éliminé ? ( 6
heures)
|
|
|
Étude
numérique.
On admet que la concentration, exprimée en mg/L , du produit actif dans
le sang du malade est donnée en fonction du temps t , exprimé en
heures, par la fonction f définie sur l’intervalle [0 ; 6] par : f (t )
= t3 −12t2 +36t .
Reproduire
et compléter le tableau de valeur numérique.
| t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| f(t) |
0 |
1-12+36
=25 |
23-12*22+36*2
=32 |
33-12*32+36*3
=27 |
43-12*42+36*4
=16 |
5 |
0 |
On note f ′ la
fonction dérivée de la fonction f sur l’intervalle [0 ; 6].
Calculer
f ′(t ).
f '(t) = 3t2-12*2t +36 = 3t2-24t
+36
Démontrer
que, pour tout nombre réel t de l’intervalle [0 ; 6], on a : f ′(t )=
(t −6)(3t −6).
f '(2) = 3*22-24*2+36 = 0, donc 2 est une racine
de 3t2-24t
+36=0.
f '(6) = 3*62-24*6+36
= 0, donc 6 est une racine de 3t2-24t
+36=0.
par suite f '(t) =a(t-6)(t-2)
Développer a(t2-8t+12) = 3t2-24t
+36. On en déduit a = 3.
Résoudre
l’équation f ′(t ) = 0 sur l’intervalle [0 ; 6].
La dérivée s'annule pour x=2 et x = 6.
Étudier
le signe de f ′(t ) sur l’intervalle [0 ; 6].
Sur [0 ; 2[ la dérivée
est positive ; sur ]2 ; 6[, la dérivée est négative.
Construire
le tableau de variations de la fonction f sur l’intervalle [0 ; 6].
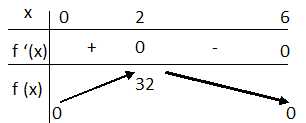
En
déduire la concentration maximale du produit actif dans le sang du
malade.
f(2) =23-12*22+36*2
=32 mg/L.
|
.
|
|
On
considère la fonction f définie sur l’intervalle [−5 ; 10] dont la
représentation graphique C est donnée dans le repère orthonormal
ci-dessous. La droite (D) esttangente à la courbe au point A d’abscisse
5.
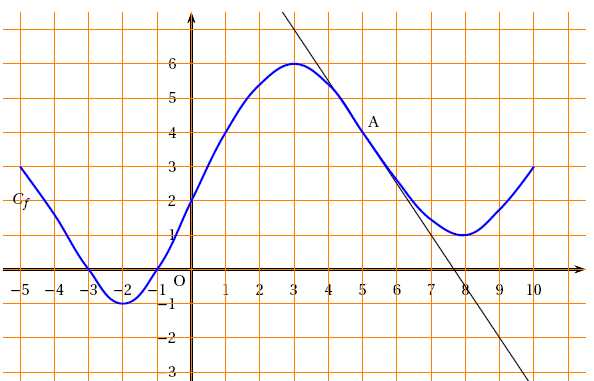
L’ensemble des solutions de l’inéquation f (x)>0 est : a. [0 ; 10] ;
b. [−5 ; −3] et [−1 ; 10] c. [−2 ; 3] et [8 ; 10].
f(x) est positive entre -5 et -3 ainsi qu'entre -1 et 10
L’ensemble des solutions de l’équation f (x) = 0 est : a. {2} ;
b. {−3 ; −1} ; c. {−2 ; 3 ; 8}.
f(x) est nulle pour x =-3, x=-1.
Le nombre dérivé de la fonction f en x = 5 est égal à : a. 5 ; b.
-1,5 ; c. −2.
Le nombre dérivé est égal à la pente de la droite D, c'est à dire -1,5.
On considère la fonction g définie sur l’intervalle [0 ; +1[ par g (x)
= 2500×0,7x .
L’image, arrondie à l’unité, de 5 par la fonction g est égale à : a.
420 ; b. 8 750 ; c. 7 500.
g(5) =2500*0,75 =420.
Les
solutions de l’inéquation g (x)< 100 sont les nombres réels x tels
que : a. x>log 0,04 / log 0,7 ; b. x<log0,04 / log 0,7 ; c.
x<log 0,7 / log 0,04.
2500×0,7x<100 ; 25x0,7x<1
; 0,7x<0,04
; x lg 0,7 <log 0,04 ; x(-log 0,7) < (-log 0,04) ; x > log 0,04 / log 0,7.
|
|