Probabilités,
bac.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Dans
un lycée donné, on sait que 55% des élèves sont des filles. On sait
également que 35% des filles et 30% des garçons déjeunent à la cantine.
On choisit au hasard un élève du lycée.
Quelle
est la probabilité que cet élève ne déjeune pas à la cantine ?
On
note Fille l'évenement " l'élève choisi est une fille", Garçon
l'évenement "l'élève est un garçon" et Cantine l'évènement " l'élève
déjeune à la cantine".
p(Fille) = 0,55 ; p(garçon) = 1-0,55 = 0,45.
pfille(Cantine) =0,35 et pgarçon(Cantine) = 0,30.
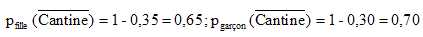
Construisons un arbre :

|
|
|
Une urne contient dix jetons
numérotés de 1 à 10, indiscernables au toucher. On tire 3 jetons
simultanément.
Combien
de tirages différents peut-on faire contenant au moins un jeton à
numéro pair ?
Nombre de tirages simultanés de 3 jetons parmi 10 jetons contenus dans
l'urne :
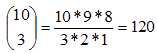
Nombre de tirages simultanés de 3 jetons parmi 5
jetons portant un numéro impair contenus dans l'urne :
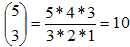
Nombre de tirages simultanés de 3 jetons parmi
10 jetons portant au moins un numéro pair contenus dans l'urne :
120-10 = 110.
On peut faire 110 tirages différents de 3 jetons parmi 10 jetons portant au moins un numéro pair.
|
| .
. |
.
|
|
Une variable aléatoire Y
suit une loi binomiale de paramètres 20 et 0,2.
Calculer
la probabilité que Y soit supérieure ou égale à 2. Donner une valeur
approchée du résultat à 10−3.
Soit un entier naturel k compris dans
l'intervalle [0 ; 20].
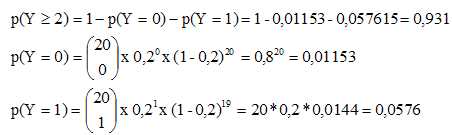
Un appareil ménager peut présenter après sa fabrication deux défauts.
On
appelle A l’événement « l’appareil présente un défaut d’apparence » et
F l’événement « l’appareil présente un défaut de fonctionnement ».
On suppose que les événements A et F sont indépendants.
On
sait que la probabilité que l’appareil présente un défaut d’apparence
est égale à 0,02 et que la probabilité que l’appareil présente au moins
l’un des deux défauts est égale à 0,069.
On choisit au hasard un des appareils.
Quelle
est la probabilité que l’appareil présente le défaut F ?
p(A) = 0,02 ; 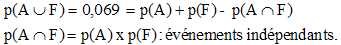
0,069 = 0,02 +p(F)-0,02 p(F).
0,069-0,02 = 0,98 p(F) ; p(F) = 0,049 /0,98 = 0,05.
|
On
considère l’algorithme :
A et C sont des entiers naturels,
C prend la valeur 0
Répéter 9 fois
A prend une valeur aléatoire entière entre 1 et 7.
Si A > 5 alors C prend la valeur C + 1
Fin Si
Fin répéter
Afficher C.
Dans l’expérience aléatoire
simulée par l’algorithme précédent, on appelle X la variable aléatoire
prenant la valeur C affichée.
Quelle loi suit la variable X ? Préciser ses paramètres.
On effectue n = 9 fois la même expérience, c'est à dire choisir au
hasard u nombre compris entre 1 et 7.
Deux éventualités sont possibles :
le succés : le nombre A est égal à 6 ou à 7 ; la probabilité vaut p =2/7
l'échec : le nombre A est compris entre 1 et 5 ; la probabilité vaut
1-2/7 = 5 / 7.
De
plus la probabilité d'obtenir 6 ou 7 est constante, quels que soient
les expériences précédentes. les expériences sont indépendantes les
unes des autres.
Le compteur C ou la variable X donne le nombre d'expériences conduisant
à un succés.
X suit la loi binomiale de paramètre n=9 et p = 2/7.
|
.
|