différencier
les 4 équations du prisme
cos i di =dn sin r + n cos r dr
(1)
cos i' di' =dn sin r' + n cos r' dr'
(2)
dA= dr + dr'
(3)
dD = di + di' - dA
(4)
pour éliminer di'
on ajoute : (1)
cosr'
+ (2) cos r
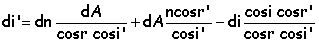
on remplace dans
(4)
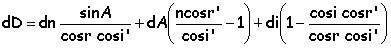
variation
de D en fonction de l'indice
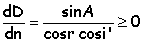
La
déviation varie dans le même sens que
l'indice
variation
de D en fonction de l'angle d'incidence
i
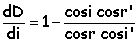
extrémum si cos i cos r' = cos i' cos
r
élever au carré et exprimer r et
r' en fonction de i et i'
soit D présente un minimum pour i =
i'
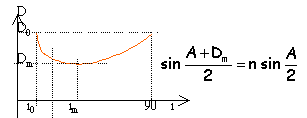
au
minimum de déviation le trajet du rayon
lumineux est symétrique par rapport au plan
bissecteur du prisme
A
petit et faibles incidences
tous les angles sont
petits : on remplace les sinus par les angles
exprimés en radians
i=nr et i'=nr' d'où
D = n(r+r')-A = (n-1)A