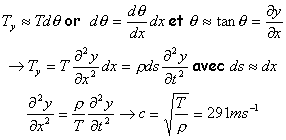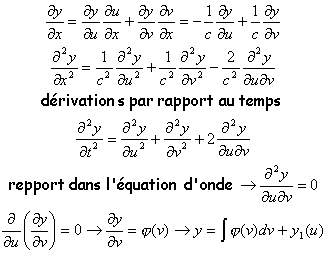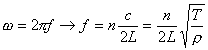ondes

	. .
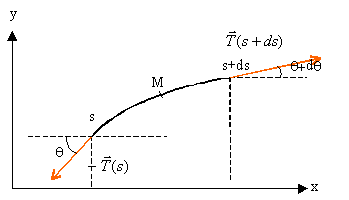
notions de base (quiz) ondes sonores ondes électromagnétiques	Propagation d'ondes sur une corde tendue d'après Capes 94 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. L'élément de corde se meut sous l'action des forces de tension tangentes à la corde aux points d'abscisses x et x+dx.
1 équation d'ondes	Une corde de longueur L, de masse linéique r, homogène est tendue. Le poids de la corde est négligé devant la tension. Au repos la corde est confondue avec l'axe Ox. En utilisant la relation fondamentale de la dynamique, appliquée à l'élément ds de la corde, écrire 2 relations faisant intervenir les tensions et les angles. Les angles restant petits et la corde s'écartant peu de l'axe Ox, montrer que la norme de la tension est constante. Ecrire l'équation d'onde; exprimer la vitesse de propagation des ondes et calculer c si L= 33 cm ; m= 0,3 g et T= 77 N. corrigé
	L'élément de corde a une masse élémentaire dm=rds. Projeter la relation fondamentale de la dynamique sur les axes Ox et Oy. équation d'onde : selon Oy : T_y= T sin(q+dq)-Tsinq. T_y= T sinq cos(dq)+Tcosq sin(dq))-Tsinq Le déplacement s'effectue suivant Oy les ondes sont transversales.
2 ondes stationnaires	La corde étant de longueur finie, les ondes se réfléchissent à ses extrémités et on peut observer sous certaines conditions un phénomène d'ondes stationnaires Si y₁(x,t) est une onde progressive se déplaçant ves les x croissants et y₂(x,t) une onde progressive se déplaçant vers les x décroissants, écrire l'onde résultante y(x,t) en un point M en ne tenant compte que d'une seule réflexion. Les extrémités de la corde étant fixes, montrer que seules certaines fréquences sont compatibles avec les conditions imposées. Exprimer ces fréquences en fonction de T, r et L. Calculer la valeur de la fréquence la plus faible. Comment choisir une corde pour qu'elle puisse rendre des sons graves ou aigus ? corrigé
	Montrons qu'une solution de la forme : y(x,t) = y₁(t-x/c) + y₂(t+x/c) est solution de l'équation d'onde. Effectuer le changement de variable u=t-x/c et v=t+x/c L'onde résultante s'écrit : y(x,t)= y₁ cosw(t-x/c)+ y₂ cos w (t+x/c) y(0,t)=0 quel que soit t : y₁ cos(wt)+ y₂ cos (w t)=0--->y₁= -y₂ y(L,t)=0 quel que soit t : y₁ [cosw(t-L/c)_- cos w (t+L/c)]=0--->wL/c=np les fréquences cherchées sont : la fréquence la plus faible correspond à n=1 : f=441 Hz. Sons graves(fréquences basses) : corde massive. Sons aigus (fréquences élevées) : corde légère. Accorder consiste à régler la tension de la corde.
3 ondes stationnaires	On considère une onde plane incidente, de longueurd'onde l, réfléchie par un obstacle B parfaitement réfléchissant (R=1) placé à l'origine x=0 et normal à la direction de propagation. En appelant ''A'' l'amplitude de l'onde incidente, et en supposant nul le déphasage à la réflexion, donner l'expression z_i((x,t) et z_r(x,t) de l'onde incidente et de l'onde réfléchie. - Calculer l'amplitude A(x) de l'onde résultante en un point de côte x. - Quelle est sa valeur en x=0, point B, obstacle où se produit la réflexion. - Donner la valeur et la position des maxima et des minima d'amplitude. - Quelle en est la périodicité spatiale? Quelles sont les nouvelles positions des maxima et des minima d'amplitude si l'obstacle déphase l'onde incidente de F ? Connaissant les positions x₁ et x₂ des deux premiers minima consécutifs, calculer F. corrigé Onde incidente émise par la source S: z_S(x,t)= A sin(wt) avec w = 2p/T; T : période en seconde. l'obstacle en B est supposé fixe : * si le point B pouvait vibrer, l'onde incidente lui ferait reproduire le mouvement de la source : z_{B incidente}(0,t)= A sin(wt) * B étant immobile, il y a en B superposition de deux mouvement vibratoires, l'onde incidente et l'onde réfléchie : z_{B réfléchie}(0,t)= -A sin(wt) de telle sorte que : z_{B incidente}(0,t)+ z_{B réfléchie}(0,t)=0. Soit un point M situé à la distance x de B : l'onde incidente atteind le point M avant le point B; l la vibration de M présente une avance de q =BM/v = x/v sur celle de B; v: célérité de l'onde en m/s ; l : longueur d'onde en m. soit z_{M, incidente}(x,t)=A sin(w(t+q))=A sin(2p(t/T+x/(vT)))=A sin(2p(t/T+x/l)) La vibration réfléchie en M présente un retard q =BM/v = x/v sur celle de B. z_{M, réfléchie}(x,t)= -A sin(2p(t/T-x/l)) ; L'onde résultante s'écrit : z_M(x,t)= A sin(2p(t/T+x/l))+ (-A )sin(2p(t/T-x/l)) or sin p - sin q = 2cos (( p+q)/2) sin (( p-q )/2) p =(2p(t/T+x/l)) : q=(2p(t/T-x/l)) ; ½(p+q)= 2pt/T ; ½(p-q)=2px/l z_M(x,t)= 2A sin(2px/l) cos(2pt/T) amplitude de l'onde résultante : 2A sin(2px/l). phase de l'onde résultante : 2pt/T, indépendante de x. noeuds et ventres d'élongation : l'amplitude est nulle pour : 2px/l = kp soit x_mini= ½kl.avec k=0,1, 2, 3... il y a donc un noeud en B et la distance entre deux noeuds consécutifs est : ½l. l'amplitude est maximale pour : 2px/l = (2k+1)½p soit x_maxi= (2k+1)p/4 avec k=0,1, 2, 3.. la distance entre deux ventres consécutifs est : ½l. même méthode si : l'extrèmité B est libre : z_{M, réfléchie}(x,t)= A sin(2p(t/T-x/l)) ; avec sin p + sin q = 2cos (( p-q)/2) sin (( p+q )/2) p =(2p(t/T+x/l)) : q=(2p(t/T-x/l)) ; ½(p+q)= 2pt/T ; ½(p-q)=2px/l z_M(x,t)= 2A cos(2px/l) sin(2pt/T) l'obstacle en B introduit un déphasage F de l'onde réfléchie : z_{M, réfléchie}(x,t)= A sin(2p(t/T-x/l)+F) ; p =(2p(t/T+x/l)) : q=(2p(t/T-x/l)+F) ; ½(p+q)= 2pt/T+½F ; ½(p-q)=2px/l-½F z_M(x,t)= 2A cos(2px/l -½F ) sin(2pt/T +½F ) retour - menu