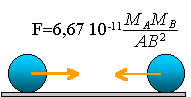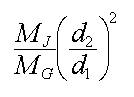| |
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
| |
|
||||||
|
|
boules de pétanques |
Deux boules de pétanques de masse 650 g sont posées l'une à côté de l'autre sur le sol. La distance de leurs centres est 20 cm
corrigé |
|||||
| |
masse en kg : 650 g = 0,65 kg distance AB en mètres : 20 cm = 0,2 m F=6,67 10-11*0,65*0,65 / 0,2² = 7 10-10 N. P = m g Poids en N, masse en kg, g= 9,8 N kg-1 à la surface de la terre P=0,65*9,8 = 6,37 N. La force de gravitation sexerçant entre les boules est négligeable devant le poids. 
|
||||||
| . . | |||||||
|
un satellite de Jupiter |
Ganymède, un satellite de Jupiter a une trajectoire circulaire de rayon 1,07 106 km centrée sur le centre de Jupiter. La sonde Voyager I est passée en 1979 entre Jupiter et ce satellite à 1,15 105 km de Ganymède.
masse Ganymède : 1,49 1023 kg ; masse Jupiter : 1,9 1027 kg
corrigé |
||||||
| |
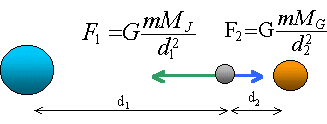
rapport des deux forces F1 / F2 :
rapport des masses : 1,9 1027 / 1,49 1023 =1,27 104. d1=1,07 106 -1,15 105 =9,55 108 m d2 =1,15 108 m rapport des distances : 1,15 108 / 9,55 108 = 0,12 rapport des forces : 1,27 104 * 0,122 = 184.
|
||||||
|
pesanteur à la surface de Io |
corrigé |
||||||
| |
pesanteur à la surface de Io : 6,67 10-11 *8,933 1022 / (1,8 106)2 6,67*8,933 1011 /(1,8*1,8 1012) 6,67*8,933 / (1,8*1,8 10) =1,84 N kg-1. environ 5,33 fois plus faible qu à la surface de la Terre. poids à la surface de Io : masse en kg : 0,5 kg 0,5*1,84 = 0,92 N poids à la surface de la Terre, 5,33 fois plus grand soit : 4,9 N
|
||||||
|
navette spatiale entre la Terre et la Lune |
On considère une navette spatiale, de masse 1800 kg, se trouvant entre la Terre et le Lune. On appelle d la distance du centre de la Terre à la navette et D la distance des centres de la Terre et de la Lune. Mterre = 6 1021 tonnes. Mlune = 1 / 83 Mterre. D=380 000 km.
corrigé |
||||||
| |
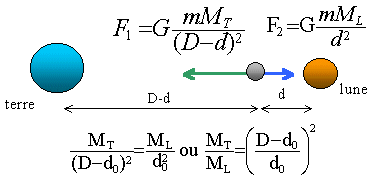
rapport des deux masses (Terre / Lune ) =83 prendre la racine carrée : 9,11 faire les produits en croix d'où : 9,11 d0=D-d0. 10,11 d0 = D d0 =380 000 /10,11 = 37 586 km à peu près le dixiéme de la distance Terre Lune, plus proche de l'astre le plus petit. |
||||||
|
3ème loi de Kepler |
Les lois du mouvement des planètes du Soleil ont été énoncées par J. KEPLER,astronome allemand(1571-1630) et portent son nom. La 3ème loi est la suivante:
|
||||||
| |
365² /(1,5 108 )3 = 3,94 10-20 jour² km-3. rayon de l'orbite de Mars : 1,52*1,5 108 = 2,28 108 km
T²= 3,94 10-20 * (2,28 108) 3 =46,69 104 jours ² T= 683 jours terrestres vitesse = circonférence en km / durée en jours 2*3,14 *2,28 108 / 683 = 2,1 106 km jour-1. |
||||||
| |
|
||||||
| |
|
||||||
|
|
|
||||||