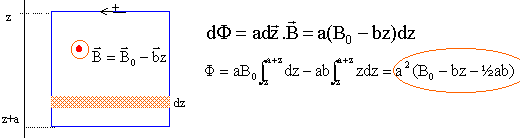Aurélie 01/02
chute d'un cadre dans un champ magnétique variable

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

  1. On étudie la chute d'un cadre (carré de coté a) dans un champ magnétique. Le cadre est placé dans un plan vertical et le champ est perpendiculaire au plan du cadre. A l'instant t=0 on libère le cadre dont la vitesse initiale est nulle et dont deux cotés sont horizontaux ; le coté supérieur est situé à la cote z.=0.

    - Calculer en fonction de la cote z du coté supérieur du cadre le flux d'induction F dans ce cadre.
    - Indiquer sur la figure le sens du courant induit dans ce cadre. Expliquer. En déduire les forces électromagnétiques.
    - Calculer en fonction de la vitesse de chute dz/dt = z' la fem d'induction, l'intensité du courant induit et la résultante des forces électromagnétiques s'exerçant sur le cadre.

  2. Ecrire et résoudre l'équation différentielle régissant la chute du cadre. On exprimera les résultats en posant t =mR/ (b2a4).
    application numérique : R = 10-3 ohm ; m= 10,24g ; b=6,4 SI; a= 10cm ; g= 10m/s².
    - Que peut-on dire du mouvement du cadre ?
  3. A partir du temps t =10 s on fait diminuer l'induction du champ magnétique dont la valeur devient B=B0-bz-b1(t-10).
    - écrire et résoudre la nouvelle équation du mouvement. On exprimera les résultats en posant g= bb1a4/ (Rm). On peut faire le changement de variable T=t-10 et Z=z-z10.
    - application numérique : valeurs identiques ; b1 = 0,256 SI. Quel est le mouvement du cadre ?
    - tracer en fonction du temps la cote z entre t=0 et t=13 s.
corrigé
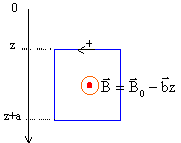
le vecteur surface est orienté d'après le sens de parcours choisi sur le contour C. Dans ce cas le vecteur surface et le vecteur champ magnétique sont colinéaire et de même sens.

expression du flux :

faire le calcul pour une surface de largeur dz, de longueur a, située à la cote z, puis intégrer entre z et a+z.

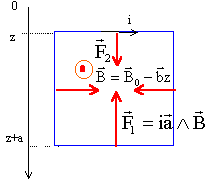
Un courant induit prend naissance dans ce cadre et par ces effets électromagnétiques il va s'opposer à la chute du cadre. La résultante des forces électromagnétiques sera verticale vers le haut, d'où le sens du courant induit.

Les forces qui s'exercent sur le cotés verticaux sont opposées.

norme de F1 : ia(B0-b(a+z))

norme de F2 : ia(B0-bz)

norme de la résultante des forces : F = ia²b

fem dinduction et courant induit :

e = - dF/dt = a²b dz/dt = a²b v avec v= dz/dt = z'.

intensité du courant : i = e/R = a²b/R v.

résultante des forces électromagnétiques : F =a4b2/R v.

mouvement du cadre :

relation fondamentale de la dynamique appliqué au cadre ( repère terrestre galiléen)

-F + mg = -a4b2/R v + mg = mz"

diviser par m et faire intervenir t =mR/ (b2a4).
z" + z' / t = g ou bien v' + v/ t = g. (1)

résolution de cette équation différentielle :

solution générale de l'équation sans second membre : v = A exp( -t /t )

solution particulière de (1) :

la vitesse limite est égale à gt .

solution générale de (1) :

v = A exp( -t /t ) + gt .

déterminer A en écrivant qu'à t=0 la vitesse est nulle d'où 0 = A +gt .

v = gt ( 1- exp( -t /t )).

application numérique : m = 1,024 10-2 kg ; a = 0,1 m

t = 10-3 * 1,024 10-2 / (10-4 *6,4²) = 2,5 10-3 s

v = 2,5 10-2 (1 -exp( - 400 t))

la vitesse limite est très rapidement atteinte et le mouvement du cadre est uniforme.

alors z = gt t = 0,025 t et z10 = 2,510-2*10 = 0,25 m

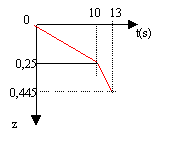
nouvelle expression du flux : F1=F -a²b1T

e = - dF1/dT= a²b dZ/dT -a²b1 = a²b v -a²b1.

intensité = e/ R= a²/ R(bv - b1)

résultante des forces : F= a² b i = a4/R(b²v-bb1)

équation différentielle du mouvement :

-F+mg = mv' soit -a4/R(b²v-bb1) +mg = mv'

diviser par m, faire intervenir t =mR/ (b2a4) et g= bb1a4/ (Rm).

v' + v/t = g+g

ou Z" + Z' /t = g+g (2)

valeur numérique de g : 6,4*0,256 10-4 / (1,024 10-5)= 16 (du même ordre de grandeur que g)

résolution de cette équation différentielle :

solution générale de l'équation sans second membre :

équation caractéristique r²+r /t =0 ( r1=0 et r2 = -1 /t)

Z = A +B exp(-T /t)

solution particulière de (2 ) :

Z' = (g+g )t . d'où Z = (g+g )tT

solution générale de (2) :

Z = A +B exp(-T /t) +(g+g )tT

déterminer A et B :

à T=0, Z=0 d'où A= -B

Z = A( 1- exp(-T /t) ) + (g+g )tT

à T=0 la vitesse est Z' = gt .

Z' = A/t exp(-T /t)+ (g+g )t

gt =A/t + (g+g )t d'où A = -g t² .

Z = -g t² ( 1- exp(-T /t) ) + (g+g )tT

Z = -16* (2,5 10-3 )²(1-exp (-400T) )+ 26*2,5 10-3 T

Z = -10-4 (1-exp (-400T))+ 0,065 T voisin de -10-4 + 0,065 T.

le mouvement devient rapidement uniforme avec une vitesse limite égale à 0,065 m/s.

Z(T=3s) = 0,195 m soit z (t=13) =0,25+0,195 = 0,445 m

retour - menu