|
Capes 97 exercice suivant (spire dans un champ magnétique non uniforme) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||
|
||
|
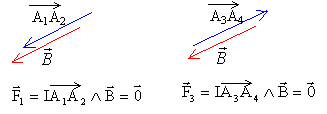
préalable : On admet le résultat qui suit : En partant de la force de Lorentz f subie par une particule de charge q, de vitesse v, placée en M où existe un champ magnétique B, on peut aboutir à la loi suivante: Une portion de courant rectiligne MN, parcourue par un courant d'intensité I, mesuré dans le sens M vers N, placé dans un champ magnétique uniforme B, est soumis à une force F, appliquée en son milieu Q. 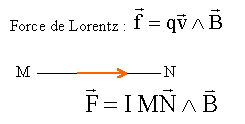 Quelle est le nom donné à cette force? spire plane dans un champ magnétique uniforme : Une spire rigide de côté a, d'arie S est
parcourue par un courant d'intensité I imposée
par le générateur. On défini son moment
magnétique : La spire de centre M, mobile sans frottement autour d'un axe D=Mz est placée dans un champ magnétique uniforme B, ayant la direction et le sens de l'axe Mz. Sa position est repèrée par l'angle q. 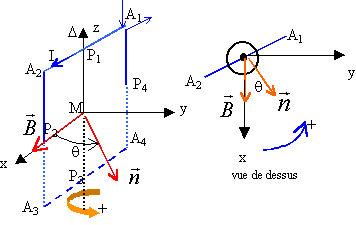
|
||
|
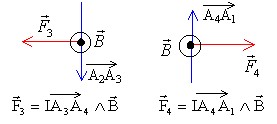
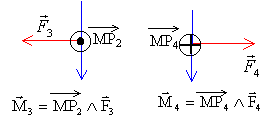
la somme des forces est donc nulle. les deux forces F3 et F4 constituent un couple de forces dont l'effet est la rotation de la spire. Le moment de ces forces par rapport à l'axe D, est égal à la projection sur cet axe, du moment de ces forces par rapport à un point de cet axe.(le point M par exemple)
le moment des forces est dirigé en sens contraire de l'axe Oz sa valeur est (a² représente la surface S de la spire) MD = -Ia² B sin q= - I S Bsin q. énergie potentielle: La spire tourne d'un angle dq autour de Mz, l'intensité restant constante. le travail élémentaire du couple de forces est : dW = MD dq = -IS B sinq dq = -d [ -IS B cosq ] on défini une énergie potentielle d Ep = - dW = -d [ IS B cosq ]
énergie potentielle magnétique d'interaction d'un dipole avec un champ magnétique. La position d'équilibre stable correspond à un minimum de l'énergie potentielle : dEp / dq = M B sin q = 0 soit q =0 ou q =p. ces deux positions d'équilibres sont-elles stables ? recherchons le signe de la dérivée seconde : d²Ep / dq ²= M B cos q la dérivée seconde est positive pour q=0, cet équilibre est stable. la dérivée seconde est négative pour q=p, cet équilibre est instable. Dans la position correspondant à l'équilibre stable, on retrouve la règle du flux maximal : un circuit non déformable, parcouru par un courant d'intensité constante, se déplace spontanément de telle manière que le flux du champ magnétique soit maximal (sous réserve que les contraintes mécaniques imposées au circuit le permettent) Dans une aiguille aimantée, le moment magnétique résultant du aux électrons n'est pas nul et son sens détermine les pôles. En présence d'un champ magnétique uniforme, l'aiguille s'oriente et indique le sens du champ. Un grain de limaille de fer placé dans ce même champ magnétique acquiert un moment magnétique et s'oriente dans la direction du champ.
retour - menu |