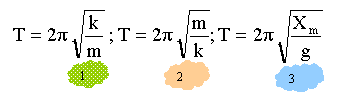|
Antilles 09/00 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
dispositif et graphes : Sur un banc à coussin d'air horizontal, un palet de masse m = 45 g est accroché à un ressort de raideur k ; l'autre extrémité du ressort est fixe. La masse du ressort est négligée. La position du centre d'inertie est repérée par son abscisse x mesurée à partir de la position d'équilibre ( à x=0 le ressort n'est ni allongé ni comprimé). Le palet est écarté de sa position d'équilibre avant d'être lâché. 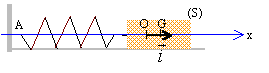
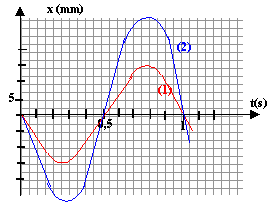
On réalise deux enregistrement avec le même ressort et le même palet.
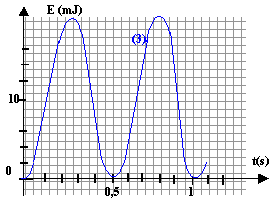
La figure ci-dessous représente l'une des forme de l'énergie en fonction du temps.
Questions :
|
||||||||||||||||||||||||||
|
k / m : [kg] [s]-2[kg]-1soit [s]-2. prendre la racine carrée :[s]-1. on trouve l'inverse de la période l'expression (3) est incorrecte: d'après les graphes (1) et (2) la période est indépendante de l'amplitude Xm. La période est donnée par la relation (2). raideur : valeur de la période, lecture graphique : T=1 s masse en kg soit 0,045 kg 1= 4 p² m / k d'où k= 4p²m= 4*3,14²*0,045 = 1,77 N/m. énergie : En absence de frottement, l'énergie mécanique est constante l'énergie cinétique est maximale pour x=0, passage à la position d'équilibre l'énergie potentielle élastique est nulle à la position d'équilibre. Ep = ½ kx². cette énergie potentielle élastique est maximale lorsque x=amplitude = 15 mm = 0,015 m L'énergie mécanique se trouve alors intégralement sous forme potentielle. Em = 0,5 *1,77 * 0,015 ² = 0,199 mJ. lecture graphe (3) : 0,2 mJ ces deux valeurs sont compatibles. L'énergie mécanique est constante : graphes (1) et (2) , l'amplitude ne diminue pas au cours du temps donc il n'y a pas d'amortissement. Au passage à la position d'équilibre (x=0) l'énergie mécanique se trouve intégralement sous forme cinétique : 2 10-4 = 0,5 mv² = 0,5 *0,045 v² v² = 2 10-4 / 0,0225 = 0,0088 vmax = 0,094 m/s.
donc énergie mécanique (2) = 4 énergie mécanique (1) ** l'énergie potentielle élastique est identique aux dates citées. L'énergie mécanique en (2) est 4 fois plus grande qu'en (1) l'énergie mécanique est la somme des énergies potentielle et cinétique donc Ec(2) > Ec(1). *** L'énergie cinétique est proportionnelle au carré de la vitesse. A la plus grande énergie cinétique correspond la plus grande vitesse
|
|||||||||||||||||||||||||||
|