|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
données : la masse de chaque noyau est 2,3.10-26 kg. ; K=9.109 S.I.;G=6,7.10-11S.I.
corrigé 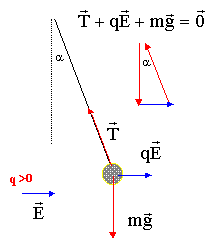
mg = 0,0025*10 = 0,025 N qE= 5 10-7 N tan 30 = qE/(mg) d'où qE= mg tan30 = 0,025*0,577 = 1,44 10-2 E= 2,88 104 V/m . tan a = 5 10 -7 * 10 4 /
0,025 = 11,3°.
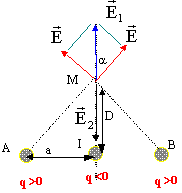
E = 9 109 q/AM² ; tan a = D/a ; E1=2 E cos a E2 = 9 109 q/D² le champ résultant est porté par la médiatrice du segment AB ; sa valeur est E2-E1. AM² = a² + D² = 0,2²+1²= 1,04 ; tan a = 1/0,2=5 ; cos a = 0,196 E = 9 109 10-9 / 1,04 = 8,65 V/m ; E1 = 2*8,65*0,196 = 3,4 V/m E2 = 9 109 10-9 / 1² = 9 V/m champ résultant en M : 9-3,4 = 5,6 V/m.
F = 9 109 q²/ d² avec d = 0,14 10-9 m F= 9 109 (1,12 10-18)² / (0,14 10-9)² = 5,8 10-7 N. force gravitationnelle toujours attractive 6,7 10-11 m²/d²: 6,7 10-11 *(2,3.10-26)²/ (0,14 10-9)² =1,8 10-42 N. dans l'infiniment petit de la molécule, les forces de gravitation sont négligeables devant les forces électriques. |
|||||
|
La distance entre la terre et la lune est de 384 000 km en moyenne. Le rapport des masses des 2 planètes est Mt/Ml=81,5. Le satellite géostationnaire Eutelsat,de masse m=985 kg.,gravite à 42 000 km du centre de la terre et se trouve entre la terre et la lune.
corrigé force gravitationnelle exercée par la terre sur la satellite situé à la distance TS= 4,2 107 m du centre de la terre F1 = GMt m/ TS² force gravitationnelle exercée par la lune sur la satellite situé à la distance LS= 3,84 108-4,2 107 = 3,42 108 m du centre de la lune (LS / TS) =8,14 F2 = GMlm/ LS² F1/F2
=Mt / Ml( LS/TS)² = 81,5 (8,14)² = 5400.
F1 = GMt Ml/ TL² force gravitationnelle exercée par le soleil sur la lune située à la distance D= 1,5.1011 m (D / TL) =390,6 F2 = GMsMl/ D² F1/F2
=Mt / Ms( D/TL)² = (390,6)² / 3,31.105
= 0,46.
Ml = 1,6 * (1,7 106)2/ 6,67 10-11 = 7 1022 kg. g = G Ml / (R +z)² avec GMl =g0R² g= g0( R/(R+z))² avec z = 2R : g= 1,6*(1/3)² = 0,17 m/s² ( 9 fois plus petit que le champ à la surface) avec z = 10R : g= 1,6*(1/11)² = 0,013 m/s² ( 120 fois plus petit que le champ à la surface)
|
||||||
|