|
théorème de l'énergie cinétique énergie cinétique d'un astéroïde étude énergétique d'un saut En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
|
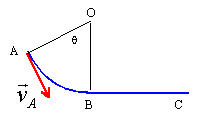
Un solide ponctuel de masse m se déplace sur la piste schématisée ci-dessous. La portion AB est un arc de cercle de rayon r, d'angle q , de centre O ; la portion BC est un segment horizontal. Les frottements sont négligés sur la partie circulaire. Sur la partie BC les frottements sont assimilables à une force constante f, colinéaire au vecteur vitesse. On lance le solide du point A avec une vitesse vA
tangente au cercle.
données : m =100g ; r = 1,5 m ; vC = vA =2 m/s; q =60° ; BC=2 m. corrigé |
||||||||||||||||||||
|
l'énergie potentielle de pesanteur diminue en passant de A en B car l'altitude de B est inférieure à celle de A. sur le plat, l'énergie cinétique diminue du fait des frottements et l'énergie potentielle reste constante. l'énergie mécanique reste constante au
cours du déplacement AB, diminue de B en C car frottement (dégagement
de chaleur)
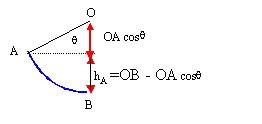
variation de l'énergie cinétique : DEc = ½mv²B -½mv²A travail du poids : mg(hA-hB) on choisit l'altitude de B comme origine de l'énergie potentielle calcul de hA: travail du poids = mgOB(1- cos q) l'action du support, perpendiculaire à la vitesse ne travaille pas DEc = ½mv²B -½mv²A = mgOB(1- cos q) diviser par la masse m et multiplier par deux : v²B -v²A = 2gOB(1- cos q) v²B =v²A + 2gOB(1- cos q) . application numérique : v²B = 4 + 2*9,8 *1,5(1-cos60) = 4 +14,7 = 18,7 prendre la racine carrée :vB
= 4,32 m/s.
la vitesse diminue entre B et C du fait des frottements : mouvement rectiligne uniformément freiné variation de l'énergie cinétique : DEc = ½mv²C -½mv²B poids et action du sol perpendiculaires à la vitesse ne travaillent pas entre B et C travail des frottements, colinéaire au vecteur vitesse mais de sens contraire. : -f BC = -f d ½mv²C -½mv²B = -f d f = ½m(v²B -v²C) / d f = 0,5*0,1 (18,7 -4) / 2 = 0,3675 N.
|
|||||||||||||||||||||
|
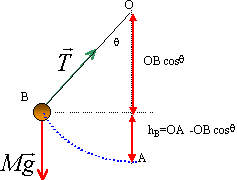
Un pendule est constitué d'une bille quasi ponctuelle de poids P =0,5 N, d'un fil de longueur L = 40 cm, de masse négligeable, attaché en O au support horizontal. Le pendule est écarté d'un angle q=60° de sa position initiale verticale, puis abandonné sans vitesse initiale. Il se met alors à osciller. 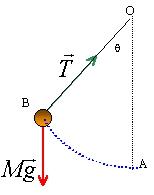
corrigé travail du poids :
A : origine des altitudes travail du poids sur le trajet BA = mg (hB-hA)= mgOA(1 -cos q) mg = 0,5 N ; L =OA = 0,4 m et q=60° W = 0,5 *0,4(1- 0,5) = 0,1 J. ce travail est nul sur une demi oscillation (même altitude de départ et d'arrivée) tension : force variable mais perpendiculaire à la vitesse donc elle ne travaille pas. en B : l'énergie mécanique est sous forme potentielle de pesanteur (énergie cinétique nulle) au passage à la position d'équilibre en A elle est sous forme d'énergie cinétique (altitude nulle) l'énergie mécanique reste constante car seul le poids travaille au cours de ce déplacement.
|
|||||||||||||||||||||
|
Une petite planète de masse m=1015 kg décrit une orbite élliptique autour du soleil S. Elle passe par le point le plus proche du soleil , appelé périhélie P0 à un instant choisi comme origine des dates. Elle parvient 39 mois plus tard au point le plus éloigné appelé aphélie et noté P13. Ses positions successives sont repérées à intervalle de temps constant. L'échelle utilisées est-elle que 1 cm correspond à 1 U.A = 1,5 1011 m. 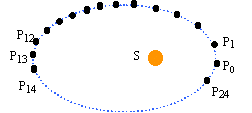
corrigé l'unité astronomique est la distance moyenne terre soleil. dans le référentiel héliocentrique ( origine le centre du soleil et les axes pointent vers des étoiles lointaines fixes) on calcule la vitesse moyenne sur le parcours P24P1 puis sur le parcours P12P14 . distance : P24P1 = 2*1,5 1011 = 3 1011 m 39 mois correspondent à 13 intervalles de temps : la durée du parcours P24P1 est de 39 /13 *2 = 6 mois durée 6 *30*24*3600 = 1,55 107 s. vitesse en P0 = 3 1011 /1,55 107= 2 104 m/s. distance : P14P12 = 1*1,5 1011 = 1,5 1011 m durée du parcours : 6 *30*24*3600 = 1,55 107 s. vitesse en P13 = 1,5 1011 /1,55 107= 1 104 m/s. énergie cinétique (J) = ½ m v² en P0 : 0,5 *1015 * 4 108 = 2 1023 J. en P13 : 0,5 *1015 * 108 = 0,5 1023 J. appliquer le théorème de l'énergie cinétique à la planète, soumise uniquement à la force de gravitation exercée par le soleil. DEc = 0,5 1023 -2 1023 - = - 1,5 1023 J travail résistant de la force de gravitation sur le premier demi tour : - 1,5 1023 J . le travail sur un tour est nul (pas de variation d'énergie cinétique sur un tour) donc travail moteur de la force de gravitation sur le second demi tour : 1,5 1023 J . |
|||||||||||||||||||||
|
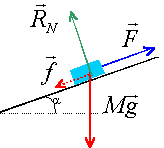
Un bloc de 80 kg est immobile en bas d'un plan incliné d'un angle de 30° sur l'horizontale (position A). Pour être hissé en haut du plan incliné, le bloc est relié à un treuil par l'intermédiaire d'une corde. La corde, parallèle au plan incliné, exerce sur le bloc une force de traction constante de valeur F=520N. Le bloc arrive en haut du plan incliné (position B) avec une vitesse de 2,20 m/s, après avoir parcouru une distance de 6,5 m.
corrigé bloc immobile au départ : énergie cinétique nulle en A à l'arrivée en B : ½mv² = 0,5*80*2,2² =193,6 J variation énergie cinétique :Ec(B)-Ec(A) = 193,6 J .
l'action du plan RN est perpendiculaire au plan et en conséquence ne travaille pas. les forces de frottement parallèle au plan vers le bas du plan travail résistant : -6,5 f force de traction parallèle au plan vers le haut du plan : son travail est moteur : 520*6,5 = 3380 J le poids, verticale vers le bas son travail est résistant, on monte la cote : mg (HA- HB) avec HA- HB = -6,5 sin 30 = - 3,25 m 80*9,8*(-3,25) = -2548 J la somme de ces 3 travaux doit être égale à la variation d'énergie cinétique : -6,5 f -2548 +3380 = 193,6 d'où f = 98,2 N Dans ce cas les frottements ne sont pas négligeables. |
|||||||||||||||||||||
|
On veut comparer la puissance moyenne développée au cours d'un saut sur place par différentes espèces. Le saut comporte deux phases. Partant d'une vitesse nulle, l'individu se détend pendant une durée t ; il quitte alors le sol en translation avec une vitesse initiale verticale v. Il s'élève alors sur une hauteur h où sa vitesse s'annule, puis retombe. On a mesuré pour des individus de différentes espèces, cette durée t et la hauteur h atteinte.
corrigé Travail du poids, résistant en montée, de l'espèce qui saute, entre l'instant du décollage et le sommet de sa trajectoire : W = - mgh avec m en kg ; g en N.kg-1 ; h en m et W en J. Puce : -4,9 10-7 *10*0,2 = -9,8 10-7 J Taupin : - 4 10-5 *10*0,3 = -1,2 10-4 J criquet : - 3 10-3 *10*0,59 = -1,77 10-2 J homme : - 70 *10*0,6= -420 J L'action de l'air étant négligeable, la seule force qui travaille pendant le saut est le poids : l'énergie mécanique reste constante . au sommet de la trajectoire, l'énergie mécanique est sous forme potentielle de pesanteur : mgh d'où ½mv²= mgh ; v² = 2gh. Puce : 9,8 10-7 J ; v = (20*0,2)½= 2 m/s. Taupin : 1,2 10-4 J ; v = (20*0,3)½= 2,45 m/s. criquet : 1,77 10-2 J ; v = (20*0,59)½= 3,43 m/s. homme : 420 J ; v = (20*0,6)½= 3,46 m/s. L'énergie nécessaire provient de la détente (le système est comparable à un ressort comprimé qui se libère). Le travail des forces musculaires au cours de la détente est l'opposé du travail du poids au cours du saut. puiisance (watt) = énergie ou travail (J) / durée (s) ; P = mgh/t Puce : 9,8 10-7 /8 10-4 =1,2 10-3 W. Taupin : 1,2 10-4 /6,4 10-4 =0,19 W. criquet : 1,77 10-2 /2,35 10-3 =7,5 W. homme : 420 J /0,233 =1,8 103 W. Puissance développée, ramenée à l'unité de masse : Puce : 1,2 10-3 /4,9 10-7 =2 449 W/kg . Taupin : 0,19 /4 10-5 = 4,75 103 W/kg . criquet : 7,5 / 3 10-3 = 2,5 103 W/kg . homme : 1,8 103 /70 = 25,7 W/kg. Les petits animaux doivent développer une puissance bien plus importante que celle calculée ci-dessus car l'action de l'air n'est plus négligeable devant leur poids. |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
|