Aurélie oct 2001

devoirs en première S

tension d'un cable

poussée d'Archimède

tableau d'évolution CuO + C

tableau d'évolution : méthode graphique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Google


.
.

Dans un montage, on remplace un fil uniquequi exerce une tension T en un point A par deux fils exerçant au même point les tensions T1 et T2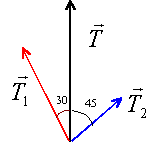

.
  1. Déterminer, par le calcul, les valeurs que doivent avoir ces tensions pour que.

    Données : T = 3,8 N .

     

corrigé

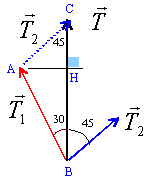
CH =AC cos 45 = AC*0,707

BH = AB cos 30 = AB*0,866

CH+BH = 3,8 (1)

AH =CH= BH tan 30 = 0,577 BH

repport dans (1)

0,577 BH +BH = 1,577 BH = 3,8

d'où BH = 2,4 et CH = 1,4

AB = 2,4 /0,866 = 2,77 N.

AC = 1,4 / 0,707 = 1,98 N


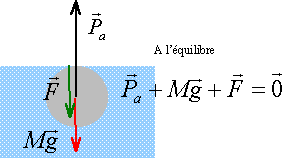
Une boule de rayon r = 5 cm, de masse volumique r, est en équilibre à la surface d'un liquide de masse volumique 0,8 g/ cm3 ou 800 kg /m3. Celle ci est à moitié immergée.

  1. Exprimer le poids de la boule.
  2. Exprimer puis calculer la poussée d'Archimède.
  3. En déduire la masse volumique du matériau constituant la boule.
  4. Quelle force verticale faut-il exercée sur la boule pour que celle-ci soit entièrement immergée et en équilibre ?

volume d'une sphère : 4/3 pr3.

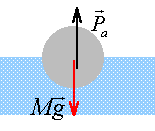
poids = poussée à l'équilibre

poids :(N) = masse (kg) *9,8

volume sphère = 4/3 *3,14 * 53 = 523 cm3.

masse (g) = volume (cm3) * masse volumique du matériau (g/cm3)

523 r en grammes soit 0,523 r kg.

poids (N) = 9,8 *0,523 r=5,125 r.

poussée : poids du volume de liquide déplacé

volume immergé : 523 /2 = 261,5 cm3.

volume immergé (cm3 )* masse volumique du liquide ( 0,8 g/cm3 ) :

261,5 *0,8 = 209,2 g ou 0,209 kg

0,209 * 9,8 = 2,04 N .

poids = poussée :

2,04= 5,125 r d'où r = 0,4 g/ cm3 = 400 kg/m3.

le poids est égal à 2,04 N

le volume immergé ayant doublé, la poussée a doublé : 4,08 N

F= 4,08-2,04 = 2,04 N. 

 


 


On fait réagir, vers 350°C, une mase m = 3,6 g de carbone avec de l'oxyde de cuivre II , de formule CuO. IL se forme du cuivre et du dioxyde de carbone (gaz).

  1. Ecrire et équilibrer l'équation de la réaction.
  2. Déterminer, à l'aide d'un tableau d'évolution :
    -a) la masse minimale, doxyde de cuivre II, nécessaire pour que tout le carbone soit oxydé.
    -b) Déterminer le volume de dioxyde de carbone recueilli, dans des conditions telles que le volume molaire a pour valeur Vm= 24 L/mol.
    -c) Calculer la masse de cuivre obtenue.

masse atomique molaire en g/mol : C=12 ; O=16 ; Cu=63,5.

corrigé
2CuO + C donnent 2Cu + CO2.

Quantité de matière de carbone : 3,6 /12 = 0,3 mol
2CuO
C
2Cu
CO2.
départ
n mol
0,3 mol
0
0
en cours
n-2x
0,3-x
2 x
x
fin
0
0
2 xmax = 0,6 mol
xmax = 0,3 mol
0,3 - xmax = 0 d'où xmax = 0,3 mol

n-2 xmax = 0 d'où n = 0,6 mol

masse molaire CuO : 63,5 +16 = 78,5 g/mol

masse CuO : 0,6 *78,5 = 47,1 g.

volume CO2 gaz : 0,3 *24 =7,2 L.

masse de cuivre : 63,5 * 0,6 = 38,1 g.

Suivi d'une transformation chimique par méthode graphique :

Le diagramme représente l'évolution des quantité de matière des espèces chimiques au cours d'une transformation chimique.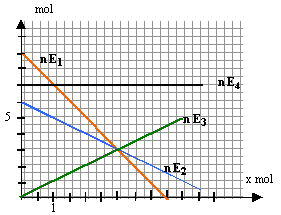

 

  1. Toutes les espèces chimiques participent-elles à la transformation?
  2. Quels sont les réactifs ?
  3. Quel est le produit ?
  4. Quel est le réactif limitant ?
  5. Quels sont les nombres stoéchiométriques ( le coefficient de E2 etant égal a 1) ?
  6. Quel est l'avancement maximal ?
  7. Quelle est la composition du système dans l'état final ?
corrigé
E4 ne participe pas : le nombre de mole reste constant

E1 et E2 réactifs : les quantités de matière diminuent

E3 produit : la quantité de matière augmente

E1 limitant : il disparaît avant E2.

avancement maxi = 4,5 mol ( intersection nE1 avec l'axe des abscisses)

les coefficients stoéchiomètriques sont, en valeur absolue, les coefficients directeurs des droites.

pour E1 : 9/4,5 = 2 .

pour E3 : 3 / 3 = 1 .

2E1 + E2 donne E3
2E1
E2
E3
départ
9 mol
6 mol
0
en cours
9-2x
6-x
x
fin
0
6-4,5 = 1,5 mol
4,5 mol

 


à suivre ...
retour - menu
à bientôt ...