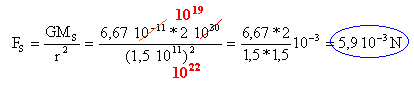|
les interactions fondamentales En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
L'acide chlorhydrique réagit sur le zinc en donnant du dihydrogène et une solution aqueuse de chlorure de zinc 2H3O+ +2Cl- +Zn -->H2 +Zn2+ +2Cl- +2H2O A la date t=0 , on introduit une masse m=1,0g de zinc en poudre dans un ballon contenant v = 40mL d'une solution d'acide chlorhydrique de concentration molaire Ca=0,50 mol.L-1.On recueille le gaz dihydrogène formé au cours du temps et on en mesure son volume V .
Zn = 65,4 g/mol ; volume molaire : 24 L/mol corrigé |
||||||||||||||||||||||||
|
zinc: masse (g) / masse molaire (g/mol) = 11 /65,4 = 15,3 mmol = 1,53 10-3 mol. acide :
volume (L) fois concentration (mol / L) = 0,04*0,5 = 0,02 mol = 20
mmol.
20-2 x max =0 soit x max =10 mmol soit 15,3- xmax = 0 d'où xmax =15,3 mmol On retient la plus petite valeur x max =10 mmol.
0,103 / 24 = 4,29 mmol = 4,29 10-3 mol le degré d'avancement est 4,9 mmol. donc la quantité de matière d'ion Zn2+ est 4,9 mmol dans un volume de solution de 40 mL. [Zn2+]= 4,9 10-3 /
40 10-3 = 0,107 mol /L.
10 mmol dans 40 mL de solution soit [Zn2+]fin= 10 10-3 / 40 10-3 = 0,25 mol /L. masse de zinc restant (g) = qTé de matière de zinc (mol) fois masse molaire (g/mol) 5,3 10-3 *65,4 = 0,35 g.
|
|||||||||||||||||||||||||
|
Une bouteille en verre , de contenance égale à 1,50 L contient de l'air à la température 20° et à la pression atmosphérique P = 1,013*105 Pa . L'air est composée d'environ 80% de diazote et de 20% d'O2 en volume . On considérera que c'est un gaz parfait .
O=16 ; N=14 g/mol ; R=8,31 SI.
corrigé équation des gaz parfaits : PV = nRT P pression en pascal ; V : volume en m3; n (mol); T température en kelvin P= 1,013 105 Pa; 1,5 L= 1,5 10-3 m3 ; T=273 +20 =293 K n = PV / (RT) = 1,03 105 *1,5 10-3 / (8,31 *293)=0,0616 mol = 61,6 mmol d'air. L'air contient en volume, donc en mole, 80% de diazote : 61,6 *0,8 = 49,3 mol N2 masse molaire N2 = 14*2=28g/mol. masse diazote : 28*0,0493 = 1,38 g. l'air contient en volume, donc en mole 20 % de dioxygène: 61,6*0,2 = 12,3 mmol O2. masse molaire O2 = 16*2= 32g/mol. masse dioxygène :
32*0,0123 = 0,39 g.
si la température augmente alors la pression augmente. P2 =
nRT2 / V =0,0616 *8,31*(273+100) / 0,0015 = 1,27 105 Pa..
Si on chauffe la bouteille une certaine quantité de gaz s'échappe. n1 = PV /(RT) = 1,013 105*0,0015 / (8,31*373) = 0,0484 mol = 48,4 mmol. 0,0484 mol d'air reste dans la bouteille soit occupe un volume de 1,5 L. volume d'une mole dans ces conditions : 1,5 / 0,0484 = 31 L /mol.
|
|||||||||||||||||||||||||
|
Un particule a est un noyau d'hélium constitué de 2 protons et de 2 neutrons.
corrigé poids : masse (kg) fois 9,8 = 6,6 10-27*9,8 = 6,5 10-25 N. la particule alpha compte deux protons positifs: sa charge est q=2e = 2*1,6 10-19 = 3,2 10-19 C. force électrostatique : U=1kV = 1000 V; d=10 cm = 0,1 m F= 3,2 10-19*1000 / 0,1 = 3,2 10-15 N. le poids de la particule alpha est négligeable devant la force électrostatique. |
|||||||||||||||||||||||||
|
On assimile le Soleil à une sphère de rayon R et de masse M présentant une répartition de masse à symétrie sphérique. On suppose que la trajectoire du centre de la Terre autour du soleil est un cercle de rayon r.
Données : R = 7 105 km; masse du soleil M = 2 1030 kg ; r = 1,5 108 km. Constante d'attraction universelle: K = 6,67 10-11 S.I. Masse de la terre : m = 6 1024 kg corrigé 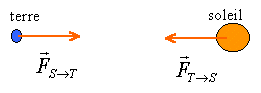
force de gravitatin exercée par le soleil sur une masse de 1kg situé à la distance r = 1,5 108 km = 1,5 1011 m.
poids d'une masse de 1 kg situé à la surface de la terre : 9,8 N. la force attractive exercée par le soleil sur une masse de 1kg placée à la surface de la terre est 1600 fois plus petite que la force attractive exercée par la terre sur cette même masse.
|
|||||||||||||||||||||||||
| |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||