|
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
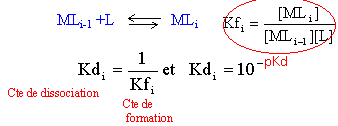
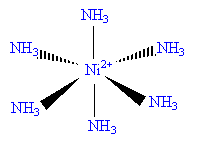
L'ion nickel Ni2+, en présence d'ammoniac NH3 peut donner six ions complexes ; les constantes de dissociations successives sont : pKd1 = 2,8 ; pKd2 = 2,44 ; pKd3 = 1,73 ; pKd4 = 1,19 ; pKd5 = 0,75 ; pKd6 = 0,03 ;
corrigé |
|||||||||||||||||||||||||||||||||||
|
La constante de formation globale bn correspond à l'équilibre : = 1,73 105 = 9,3 106 1,44 108 =8,09 108 =8,67 108 Les complexes
c4 , c5
et c6 ont des stabilités comparables
dans un milieu riche en ammoniac. Leur formation sera
pratiquement quantitative.
conservation de l'élément nickel : [c4] + [c5] + [c6] = 0,01 (1). conservation de l'élément azote : [NH3] + 6[c6] +5 [c5] +4[c4] =2,2 remplacer 4[c4] par : 0,04 - 4[c5] - 4 [c6] [NH3] + 2[c6] + [c5] =2,16 (2). équilibres successifs :
(3) fois (4) donne 5,6*1,07 = 6 = [c6] / ( [c4][NH3]² ) (6) recherche d'une équation avec [NH3] comme seule inconnue : dans (1) mettre [c4] en facteur commun et tenir compte des 3 dernières relations : [c4] (1 + 5,6 [NH3] + 6[NH3]² ) = 0,01 [c4] = 0,01 / (1 + 5,6 [NH3] + 6[NH3]² ) (3) donne [c5] = 5,6[c4][NH3] (6) donne [c6] = 6[c4][NH3]² repport dans (2) : [NH3] + 2[c6] + [c5] =2,16 [NH3] + 12[c4][NH3]² +5,6[c4][NH3]=2,16 diviser par [c4] et remplacer [c4] par son expression : (100 = 1/ 0,01) 100[NH3] (1 + 5,6 [NH3] + 6[NH3]² )+12[NH3]² +5,6[NH3]=216(1 + 5,6 [NH3] + 6[NH3]² ) dévellopper et regrouper : on note x = [NH3] 600 x3 -1104 x²-904x-216=0 diviser par 600 : x3 -1,207 x² - 1,84 x-0,34 = 0 si x voisin de 2 , le dernier terme est négligeable x ( x²-1,207 x-1,84) voisin de 0 retenir la solution positive de l'équation du second degré x = [NH3] = 2,1 mol/L [c4] = 0,01 / (1 + 5,6 [NH3] + 6[NH3]² ) = 2,5 10-4 mol/L [c5] = 5,6[c4][NH3]=2,94 10-3 mol/L [c6] = 6[c4][NH3]² = 6,6 10-3 mol/L
retour - menu |
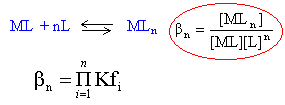
 (3)
(3)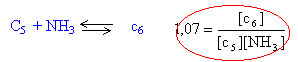 (4)
(4)