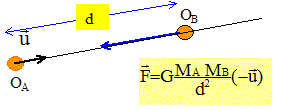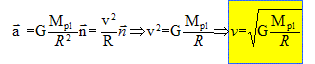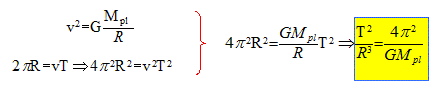|
Pluton et Charon : 3ème loi de Kepler bac S Afrique 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
Pluton a été découverte par l'astronome Clyde W Tombaugh, le 18 février 1930, après de longs mois d'observations. Pendant 66 ans, elle fut considérée comme la neuvième planète du système solaire. Cependant, depuis une quinzaine d'années, des objets semblables à Pluton de par leur taille et leur masse ont été découverts obligeant l'union astronomique internationale (UAI) à redéfinir la notion de planète. Depuis le mois d'août 2006, Pluton est classée parmi les planètes naines. Jusqu'en 1978, année de découverte du premier satellite naturel Charon, la masse de Pluton n'etait pas connue avec exactitude. Données : G = 6,673.10-11 m3.kg-1.s-2 ; 1 année sidérale = 365,2564 jours solaires moyens. 1 jour solaire moyen a une durée égale à 86 400 s. Les caractéristiques de Pluton et de Charon sont données ci-après : Pluton : rayon à l'équateur : 1,15 103 km ; distance moyenne au soleil : 5,91 109 km. Charon :
Les parties 1 et 2 de cet exercice sont indépendantes. Définir un
mouvement circulaire uniforme. La trajectoire est un
cercle ; la
norme ( valeur)
de la vitesse est
constante. Quelles sont les deux
conditions nécessaires pour observer un
mouvement circulaire uniforme ? La force doit être " centrale" : sa
direction passe par un point fixe. La valeur de la vitesse doit être
constante.
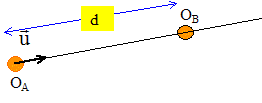
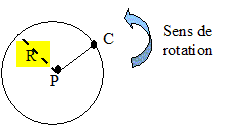
Etude du système Pluton-Charon : Le référentiel attaché à Pluton est appelé référentiel plutonocentrique. L'origine du référentiel est le centre de gravité de Pluton et ses axes sont parallèles à ceux du référentiel héliocentrique. On considère que le référentiel plutonocentrique est galiléen. Les corps célestes Pluton et Charon sont à symétrie sphérique et à répartition uniforme de masse. On néglige toutes les interactions autres que les interactions entre Pluton et Charon. On notera Mp1 la masse de Pluton, Mc la masse de Charon, P et C les centres de gravité respectifs de Pluton et de Charon. . . On fera dans un premier temps l'hypothèse que la masse de Charon est négligeable devant celle de Pluton. Le centre de gravité de Charon décrit une trajectoire circulaire de rayon R autour de Pluton. Cette trajectoire est représentée sur la figure ci-dessous. On admet que cette trajectoire est plane.
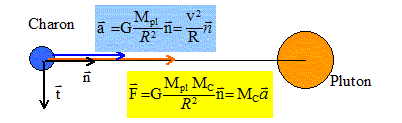
Période de révolution : Pluton met 6,387 jours solaires pour faire un tour sur elle-même et 248 années sidérales pour effectuer un tour autour du Soleil. Quelle est la période de révolution de Pluton ? Justifier la réponse. La période de révolution, est le temps mis par Pluton pour accomplir sa trajectoire, ou révolution, autour du Soleil. Pluton met 248 années sidérales pour effectuer un tour autour du Soleil. 1 année sidérale = 365,2564 jours solaires moyens ; 1 jour solaire moyen a une durée égale à 86 400 s. 248*365,2564*86400 =7,826 109 ~ 7,83 109 s. En appliquant la seconde loi de Newton au centre de inertie de Charon, en déduire les caractéristiques (direction. sens, norme) du vecteur accélération du centre d'inertie de Charon. La norme sera exprimée en fonction des données de l'énoncé.
L'accélération est centripète, dirigée vers le centre de Pluton, de valeur a= GMpl/R2. Vérifier que le mouvement circulaire uniforme est une solution de la relation établie à question précédente et montrer alors que la vitesse du centre d'inertie de Charon est : v = [GMpl/R]½. L'accélération étant centripète, l'accélération tangentielle est nulle : en conséquence la valeur de la vitesse est constante et le mouvement est circulaire uniforme.
Établir l'expression de la période de révolution T de Charon autour de Pluton. Déduire des deux questions précédentes la relation suivante : T2/R3 = 4p2/(GMpl). Charon décrit, à la vitesse v, la circonférence 2pR pendant une période T.
Cette relation traduit la 3ème loi de Kepler.
Détermination de la masse de Pluton. Expliquer ce qui a permis, à partir de 1978, de déterminer la masse de Pluton. La 3ème loi de Kepler permet de déterminer la masse de Pluton si l'on connaît la période de révolution de Charon ainsi que la masse de Charon.
Période de révolution autour de Pluton ( jour solaire) = 6,387 ; 1 jour solaire moyen a une durée égale à 86 400 s. d'où T = 6,387*86400 =5,518 105 s. distance moyenne au centre de Pluton R = 1,94 107 m. T2 =3,045 1011 s2 ; R3 = 7,30 1021 m3 ; T2/R3 = 4p2/(GMpl) donne Mpl= 4p2R3/(GT2) Mpl= 4*3,142*7,30 1021 / ( 6,67 10-11 *3,045 1011) =1,417 1022 ~1,42 1022 kg. En réalité, la masse de Charon n'est pas négligeable devant celle de Pluton. On cherche donc a calculer la masse de Pluton, notée Mp2 en tenant compte de cette nouvelle hypothèse. On montre alors que : T2/R3 = 4p2/(G ( Mp2+MC)) En déduire la masse MP2 de Pluton. Mp2= 4p2R3/(GT2)-MC = 1,417 1022 -1,61 1021 =1,256 1022 ~1,26 1022 kg. La valeur admise pour la masse de Pluton est 1,31.1022 kg. Discuter de la pertinence de l'hypothèse formulée à la question précédente. Calcul des écarts relatifs : hypothèse 1 :" masse de Charon négligeable devant celle de Pluton " : (Mpl-Mp)/Mp = (1,41-1,31) / 1,31*100 = 7,6 %. hypothèse 2: " T2/R3 = 4p2/(G ( Mp2+MC)) " : |Mp2-Mp|/Mp = (1,31-1,26) / 1,31 =3,8 %. La seconde hypothèse est plus pertinente que la première hypothèse.
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||