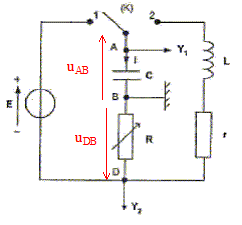
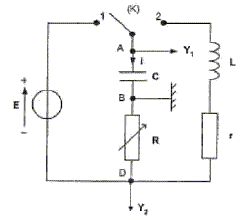Ce circuit est constitué des éléments suivants : - un générateur délivrant une tension continue constante de valeur E = 4,0 V ; - une résistance R réglable ;- un condensateur de capacité C = 2,0 µF ;- une bobine d'inductance L et de résistance r. Un commutateur (K) permet de relier le dipôle (RC) soit au générateur, soit à la bobine.

L'entrée Y₁ d'une interface, reliée à un ordinateur, est connectée à la borne A ; l'autre entrée Y₂ est connectée à la borne D. La masse de l'interface est connectée à la borne B. Les entrées Y₁ , Y₂ et la masse de l'interface sont équivalentes respectivement aux entrées Y₁ , Y₂ et à la masse d'un oscilloscope.

1. Étude énergétique du condensateur :
   Au cours de cette question, on étudie la charge du condensateur. À l'instant de date t = 0 s, le condensateur est déchargé et on bascule le commutateur en position.
   -Représenter, sur la figure, par des flèches : - la tension u_DB(t) aux bornes de la résistance ;- la tension u_AB(t) aux bornes du condensateur.
   - Charge du condensateur : Donner, en le justifiant, le signe de la charge q portée par l'armature A du condensateur au cours de sa charge et la relation existant entre la charge q et la tension U_AB.
   En tenant compte de l'orientation du circuit, donner la relation vérifiée à chaque instant par l'intensité i(t) du courant et la charge q(t).
   A partir des expressions des tensions aux bornes des trois dipôles, établir l'équation différentielle vérifiée par u_AB(t).
   Vérifier que l'expression suivante de u_AB(t) est solution de cette équation différentielle : u_AB(t) = E(1-exp(-t/(RC))
   - Énergie électrique Ee emmagasinée par le condensateur : donner en fonction de u_AB(t) l'expression littérale de l'énergie électrique E_e emmagasinée par le condensateur. En déduire l'expression littérale E_e,max de sa valeur maximale et calculer sa valeur.
2. Étude énergétique du circuit RLC :
   Une fois le condensateur chargé, l'élève bascule rapidement le commutateur (K) de la position 1 à la position 2 : il prend l'instant du basculement comme nouvelle origine des dates. Le condensateur se décharge alors dans la bobine. L'acquisition informatisée des tensions permet de visualiser l'évolution des tensions u_AB(t) et u_DB(t) en fonction du temps. Après transfert des données vers un tableur-grapheur, l'élève souhaite étudier l'évolution des différentes énergies au cours du temps.
   - Exprimer littéralement, en fonction de i(t), l'énergie magnétique E_m emmagasinée dans la bobine.
   - À partir de l'une des tensions enregistrées u_AB(t) et u_DB(t), donner l'expression de l'intensité instantanée i(t). En déduire l'expression de l'énergie magnétique emmagasinée dans la bobine en fonction de l'une des tensions enregistrées.
   - En déduire l'expression de l'énergie totale E_T du circuit en fonction des tensions u_AB(t) et u_DB(t).
   -À partir du tableur-grapheur, l'élève obtient le graphe ci-dessous (figure 2) qui montre l'évolution, en fonction du temps, des trois énergies : E_e énergie électrique, E_m, énergie magnétique et E_T énergie totale.

   Identifier chaque courbe en justifiant. Quel phénomène explique la décroissance de la courbe 1 ?

3. Entretien des oscillations :
   Pour entretenir les oscillations, on ajoute en série dans le circuit précédent un dispositif assurant cette fonction. On refait alors une acquisition informatisée.
   - Tracer sur la figure ci-dessous, les deux courbes manquantes. Préciser ce que chacune des trois courbes représente.
   - Pourquoi un tel régime est-il qualifié d'entretenu ?

   
   

   ---

   . .

---

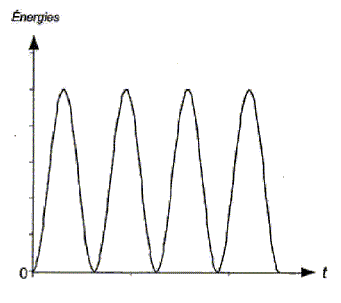
corrigé

---

Étude énergétique du condensateur :

Au cours de cette question, on étudie la charge du condensateur. À l'instant de date t = 0 s, le condensateur est déchargé et on bascule le commutateur en position.

Charge du condensateur : signe de la charge q portée par l'armature A du condensateur au cours de sa charge

L'armature B du condensateur est reliée à la borne négative du générateur ; l'armature B acquièrt une charge négative; la charge de l'armature A est donc positive.

relation existant entre la charge q et la tension U_AB :

la charge du condensateur et la tension à ses bornes sont proportionnelles : q=CU_AB
En tenant compte de l'orientation du circuit, la relation vérifiée à chaque instant par l'intensité i(t) du courant et la charge q(t) est : i(t) = dq/dt = q'

équation différentielle vérifiée par u_AB(t) :

tensions aux bornes de la résistance R : u_BD(t) = Ri = Rdq/dt = RCdU_AB/dt

additivité des tensions : E= U_AB + u_BD ; E = U_AB +RCdU_AB/dt
Vérifions que l'expression suivante de u_AB(t) est solution de cette équation différentielle : u_AB(t) = E(1-exp(-t/(RC)))

dériver u_AB(t) par rapport au temps : du_AB/dt =E/(RC) exp(-t/(RC))

repport dans l'équation différentielle : E= E(1-exp(-t/(RC))) + Eexp(-t/(RC))

cette relation est bien vérifiée que que soit t ; donc u_AB(t) = E(1-exp(-t/(RC))) est solution de l'équation différentielle.
Énergie électrique E_e emmagasinée par le condensateur :

E_e = ½Cu²_AB(t)

expression littérale E_e,max de sa valeur maximale :

la valeur maximale de u_AB(t) est E d'où : E_e,max = ½CE² = 0,5*2 10^-6*4² = 1,6 10^-5 J.

---

Étude énergétique du circuit RLC :

Expression littérale, en fonction de i(t), de l'énergie magnétique E_m emmagasinée dans la bobine :

E_m = ½Li²(t)
_{Expression de l'intensité instantanée} i(t) :

u_BD(t) = Ri ; i(t) = u_BD(t) / R ;

Expression de l'énergie magnétique emmagasinée dans la bobine en fonction de l'une des tensions enregistrées :

E_m = ½Li²(t) = ½L/R² u²_BD(t)
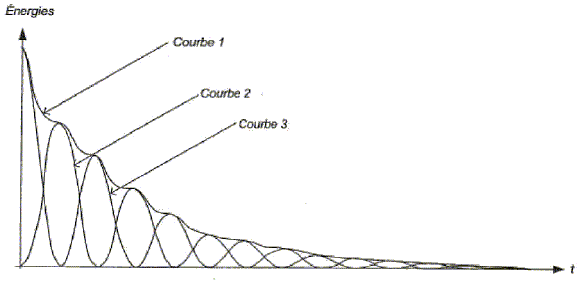
Expression de l'énergie totale E_T du circuit en fonction des tensions u_AB(t) et u_DB(t) :

E_T = E_m + E_e = ½L/R² u²_BD(t) + ½Cu²_AB(t)

courbe 3 : E_e ( à t=0, le condensateur stocke l'énergie totale du circuit)

courbe 2 : E_m ( à t=0, la bobine ne stocke pas d'énergie )

courbe 1 : E_T.

L'amplitude de la courbe 1 décroît au cours du temps : au cours des échanges d'énergie entre bobine et condensateur, une partie ce celle-ci est perdue par effet joule dans les parties résistives du circuit.

---

Entretien des oscillations :
Pour entretenir les oscillations, on ajoute en série dans le circuit précédent un dispositif assurant cette fonction. On refait alors une acquisition informatisée.

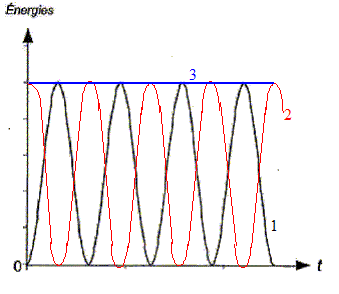
courbe 1 : E_m ( à t=0, la bobine ne stocke pas d'énergie )

courbe 2 : E_e ( à t=0, le condensateur stocke l'énergie totale du circuit)

courbe 3 : E_T = constante

Le système est entretenu : à chaque instant le dispositif électronique compense l'énergie perdue par effet joule.

---