|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
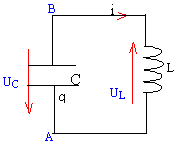
oscillations électriques : On étudie les oscillations électriques d'un dipôle constitué d'un conducteur ohmique de résistance R, d'une bobine inductive d'inductance L= 9 mH, de résistance r=2 W et d'un condensateur de capacité C=20 mF. On enregistre la tension u aux bornes du condensateur à l'aide d'un ordinateur. 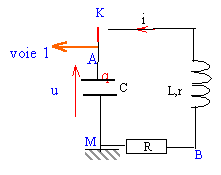 On appelle q la charge de l'armature A du condensateur et i l'intensité du courant arrivant sur l'armature A. Le condensateur étant chargé, on ferme l'interrupteur K et l'enregistrement débute. On effectue trois enregistrements de u pour les valeurs de Rf = R+r égales à 2 W, 12W, 70W. 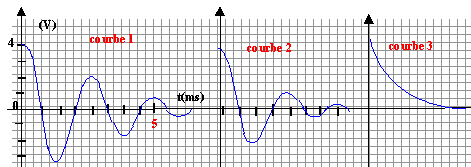
du modèle électrique au modèle mécanique : On considère un pendule horizontal constitué d'un ressort à spires non jointives, de constante de raideur k et de masse négligeable, d'un mobile autoporteur de masse m. Les frottements sont négligés. On repére l'abscisse du centre d'inertie G du système sur un axe O, x. On note v la vitesse du mobile. A l'équilibre x=0. A l'instant initial t=0 ; x=x0 positif ; v = v0 = 0. 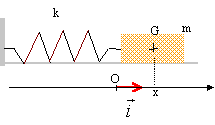 Le but de cette partie est d'établir l'expression de x en fonction du temps, dans le cas des oscillations libres du pendule. On suppose que cette expression a une forme similaire à celle de la charge q = q0 cos (wt).
validité du modèle : On dispose d'un pendule élastique horizontal de masse m = 200 g et de raideur k = 14 N/m, associé à un dispositif d'enregistrement de la variation de l'abscisse x en fonction du temps. Afin de vérifier l'exactitude du modèle mathématique on effectue le tracé théorique et l'enregistrement d'un tracé expérimental. 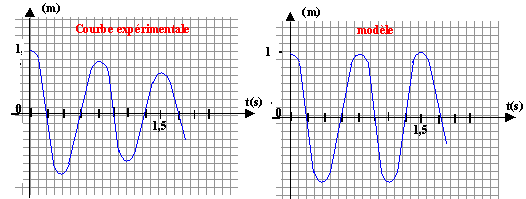
à la courbe 1 correspond la plus petite valeur de la résistance ( 2 ohms). à la
courbe 3 correspond la plus grande valeur de la
résistance ( 70 ohms)
tension aux bornes du condensateur : uC = uAB =q / C tension aux bornes de la bobine inductive : uL = uBA = L di/dt + ri le facteur ri est nul dans ce cas ( résistance totale du circuit =0) de plus i = dq/dt = q' soit i' = q" uAB +uBA = 0 soit : q/C +
Lq" = 0 où q"
+ 1/ (LC)q = 0.
L = 9 10-3 H ; C= 2 10-5 F; LC = 18 10-8. période T = 2*3,14 racine carrée (18 10-8) = 2,66 10-3 s = 2,66 ms. la pseudo-période est lue sur le graphe 1 : T' = 2,5 ms. ces valeurs sont comparables, la pseudo-période est légerement inférieure. écart
entre les deux valeurs : 0,16*100 / 2,5 = 6,4%)
avec w ² =
k/m.
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||