Cyclotron d'après IMRT En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Le premier cyclotron 1,2 MeV construit se compose d'un électro-aimant dans l'entrefer duquel on loge une boîte métallique de diamètre 28 cm ( 11 pouces) maintenue sous vide. La chambre contient deux électrodes creuses en forme de "D" entre lesquelles est appliquées une tension alternative de 4000 V à haute fréquence. En son centre se trouve une source qui fournit des protons. Les protons décrivent une trajectoire dans le plan médian, du centre jusqu'au bord. 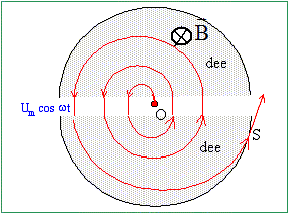Entre les dees, la seule force prépondérante est celle due à E. Dans les dees, la seule force prépondérante est celle due à B. 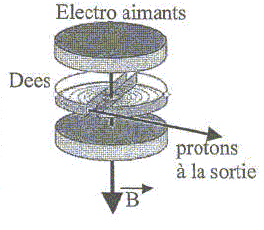Le cyclotron est constitué de deux "dees" D1 et D2 conducteurs, dans le vide desquels règne un champ magnétique uniforme constant B =2,0 T. On applique entre les dees une tension alternative sinusoîdale u(t) = Umax cos(wt) qui accélère les protons quand ils passent entre les dees. Les protons sortent d'une chambre d'ionisation au voisinage du centre O de l'appareil avec une vitesse supposée négligeable au moment où la tension appliquée entre les dees est maximale Umax =20 kV. 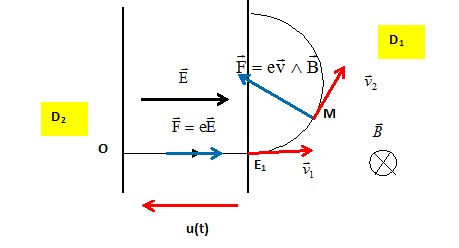B est perpendiculaire à la figure, dirigé vers l'arrière.  Donner sans démonstration la nature du mouvement des protons : - entre les deux dees. rectiligne uniformément accéléré - à l'intérieur des dees D1 ou D2 circulaire uniforme ( valeur de la vitesse constante). Représenter sur un schéma : - le champ électrique quand le proton passe de D1 à D2. Quel est à cet instant le signe de u(t) =VD2-VD1 ? - Le champ magnétique déflecteur B - les vecteurs vitesse v1 et v2 en E1 et M - la force magnétique qui s'exerce sur le proton quand il passe en M. Le champ électrique pointe vers le plus petit potentiel :VD1<VD2 ; u(t) =VD2-VD1 est donc positif. Le champ électrique pointe vers le plus petit potentiel :VD2<VD1 ; u(t) =VD2-VD1 est donc négatif. Energie et vitesse. Quelle est ( eV et J) la variation d'énergie cinétique DE des protons quand ils passent d'un "dee' à l'autre. DE = eUmax = 20 keV = 20 000 *1,6 10-19 J =3,2 10-15 J. En supposant leur énergie négligeable quand ils sont émis en O, quelle est ( eV et J) leur énergie cinétique En =f(n) quand ils sont passés n fois entre les "dees". A chaque demi-tour, à chaque passage entre les "dees, l'énergie cinétique des protons augmente de la quantité eUmax. En = 20 n keV = 3,2 10-15 n J. Quelle est alors leur vitesse v=f(n) de ces protons non relativistes ? ½mv2 =3,2 10-15 n ; v = [6,4 10-15 n / m ]½. Quel est dans ce cas le rayon R=f(n) de la traectoire ? R = mv eB = [6,4 10-15 n m ]½. eB Quel est le temps t½ mis par ces protons pour effectuer un demi-tour ? Conclure. Les protons parcourent une demi circonférence de rayon r à la vitesse v de valeur constante : p r = v t½ avec r = mv/(eB) soit r/v = m/(eB) t½ = p r v = p m eB t½ : valeur constante, indépendante de la vitesse. Quelle doit être la période T de la tension sinusoiale accélératrice ainsi que sa fréquence f ? Pour une accélération maximale, à chaque demi tour, la tension alternative doit changer de signe et prendre sa valeur maximale. La demi période de la tension alternative est égale à la durée d'un demi tour. T = 2t½ = 2p m / (eB). f = 1/T = eB /(2p m).   Vitesse finale : Les protons sortent du cyclotron avec une énergie finale ECF = 16 MeV. Combien de fois N sont-ils passés entre les "dees" ? 16 MeV = 16 000 keV. A chaque demi-tour, à chaque passage entre les "dees, l'énergie cinétique des protons augmente de la quantité eUmax. En = 20 n keV ; 16000 = 20 n ; n = 16000/20 = 800 demi-tours ; N =800 passages. Comien de tours N' auront-ils fait ? N' =½N = 400 tours. A quelle vitesse sortent-ils si on les considèrent non relativistes ? ECF =½mv2 ; v =[2 ECF/m]½ avec ECF =16 106 *1,6 10-19 =2,56 10-12 J. v =[2 *2,56 10-12/1,67 10-27]½ = 5,54 107 m/s. En réalité ces protons sont relativistes. Dans ce cas Ec = (g-1) mc2. Calculer g. g-1 = Ec /(mc2) = 2,56 10-12 /(1,67 10-27 *9 1016) =1,7 10-2 ; g = 1,017. On donne g = (1-b2)-½ avec b = v'S/c Calculer la vitesse relativiste v'S des protons. 1-b2 = 1/g2 = 1/1,0172 =0,968 ; b2 =3,31 10-2 ; b =0,182 v'S=bc =0,182 *3 108 =5,46 107 m/s. erreur relative : (5,54-5,46) / 5,54 =1,4 10-2 (1,4 %)

retour -menu