Condensateur et tube au néon concours orthoptie Rennes 2007. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

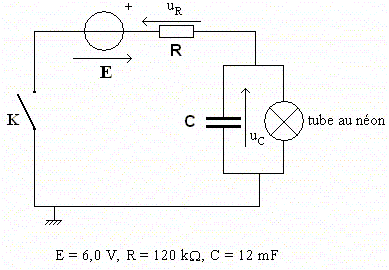
Le dipôle « tube au néon » a les caractéristiques suivantes : • Si la tension à ses bornes est nulle : il est éteint. • Il reste éteint si la tension à ses bornes reste inférieure à UA = 4,0 V. • Il s’allume si la tension à ses bornes est égale ou dépasse UA. • Une fois allumé, il ne s’éteint que si la tension à ses bornes est inférieure ou égale à UE = 2,0 V. • Lorsqu’il est éteint, le tube se comporte comme un conducteur ohmique de résistance infinie. • Lorsqu’il est allumé, le tube se comporte comme un conducteur ohmique de résistance r = 10 ohms. On réalise le montage suivant : A t = 0, on ferme l’interrupteur K. Le condensateur est initialement déchargé. Pour uC < UA, quelle est l’intensité qui traverse le tube au néon ? Justifier. Le néon est éteint si uC < UA : Etablir alors l’équation différentielle vérifiée par uC sous forme littérale. En déduire l’expression de uc(t). Le néon se comporte comme un interrupteur ouvert. Additivité des tensions : E = uR + uC avec uR =R i et i = dq/dt = CduC/dt. E = RCduC/dt + uC ; duC/dt +1/(RC) uC = E/(RC). (1) On pose t, constante de temps, t = RC Solution générale de duC/dt +1/t uC =0 : uC = A exp ( -t / t) avec A une constante. Solution particulière de (1) en régime permanent : uC = E. Solution générale de (1) : uC = A exp ( -t / t)+ E Or à t = 0, le condensateur n'est pas chargé : uC = 0 = A exp(0) + E ; A = - E uC (t)= E(1- exp ( -t / t)). A quelle date t1 le tube s’allume-t-il (expression littérale et application numérique) ? " Il s’allume si la tension à ses bornes est égale ou dépasse UA = 4,0 V". UA = E(1- exp ( -t1 / t)) ; 1- exp ( -t1 / t) = UA / E exp ( -t1 / t) = 1-UA / E ; -t1 / t = ln (1-UA / E ) t1 = -t ln (1-UA / E ). avec RC = 1,2 105 * 12 10-3 = 1,44 103 s. t1 = - 1,44 103 ln(1-4/6) =1,58 103 s ~ 1,6 103 s. Juste avant l’allumage du tube, quelle est la valeur de l’intensité débitée par le générateur ? i = C duC/dt = CE/t exp ( -t / t) ; i(t1) = E/R exp ( -t1 / t)= E/R ( 1-UA / E) i(t1) =(E-UA) / R =2 / 1,2 105 = 1,7 10-5 A. Au moment de l’allumage, que vaut l’énergie emmagasinée dans le condensateur ? Eéle = ½C U2A =0,5 * 12 10-3 * 42 =0,096 J. Comparer la constante de temps de charge du condensateur à travers la résistance R et la constante de temps de décharge du condensateur à travers le tube lorsque ce dernier est allumé. t = RC = 1,2 105 * 12 10-3 = 1,44 103 s. t' = r C = 10 * 12 10-3 = 0,12 s. t' est 12 000 fois plus petit que t : la durée de la charge est très grande par rapport à la durée de la décharge. Expliquer pourquoi pour t supérieur ou égal à t1, on peut considérer que le circuit est : La branche contenant le générateur de fem E a une résistance de 120 000 ohms ; l'intensité du courant dans celle-ci est très faible ; la branche contenant le néon allumé a une résistance de 10 ohms. Déterminer la date t2 pour laquelle le tube s’éteint à nouveau (expression littérale et application numérique). Conclure. On choisit comme origine des temps la date t1. La tension aux bornes du condensateur( décharge ) est de la forme : uC(t) = UA exp(-t/t') " Une fois allumé, il ne s’éteint que si la tension à ses bornes est inférieure ou égale à UE = 2,0 V". UE = UA exp(-t2/t') ; ln(UE /UA ) = -t2/t' ; t2= t' ln(/UA /UE ) = 0,12 ln(4/2) = 0,083 s. 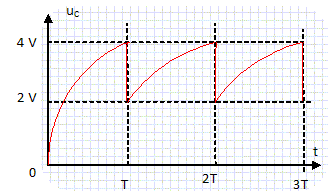Montrer qu’avec un tel circuit, uc(t) est périodique. Dès que le condensateur est éteint, la résistance de la branche contenant le néon devient infinie : cette branche se comporte comme un interrupteur ouvert. Le condensateur va donc à nouveau se charger. Dès que la tension aux bornes du condensateur atteint 4 V, le néon s'allume : le condensateur se décharge à travers le néon. Et ainsi de suite. Tracer l’allure de uc(t) sur quelques périodes. La tension E a-t-elle une influence sur cette période ? Justifier. période T = t1 + t2 ; t1 = -RC ln (1-UA / E ) ; t2= rC ln(/UA /UE ) t1 dépend de E, donc la période T dépend de E.

c

retour -menu