|
Energie d'un pendule simple : concours orthoptie ( Nantes 2008)
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
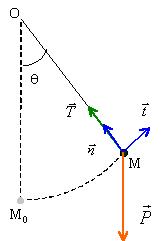
Les vecteurs sont écrits en gras et en bleu. Tracer les forces s'exerçant sur la masse m.
v = L dq/dt ; dériver par rapport au temps : dv/dt = L d2q/dt2. Ecrire les deux équations obtenues par projection de la relation fondamentale de la dynamique. mg + T = ma s'écrit en projection sur : n : T - mg cos q =mv2/L. t : 0 - mg sin q = m dv/dt. Montrer que q satisfait à une équation de la forme d2q/dt2 + w2 sin q =0. En déduire la période des petites oscillations du pendule. - mg sin q = m dv/dt = m L d2q/dt2 ; L d2q/dt2 +g sin q =0 On pose w2 = g/L d'où d2q/dt2 + w2 sin q =0. Pour les angles petits on peut confondre sin q avec q radian. d2q/dt2 + w2 q =0, équation différentielle d'un oscillateur harmonique de période T = 2p/w = 2p(L/g)½. Déterminer T en fonction de m, g, v, L et q. T - mg cos q =mv2/L ; T = m[ v2/L + g cos q ].
Déterminer l'énergie mécanique du pendule en fonction de m, g, L et q0. A la position initiale, la vitesse est nulle, l'énergie mécanique est sous forme potentielle de pesanteur. On choisit l'origine des altitudes à la position d'équilibre.
En déduire l'énergie cinétique de m pour un angle q quelconque en fonction de m, g, L, q0 et q. Energie mécanique pour un angle q quelconque : EM= mg L (1-cos q ) + Ec. En absence de frottement, l'énergie mécanique se conserve : mg L (1-cos q ) + Ec = mg L (1-cos q0 ) Ec =mg L (cos q - cos q0 ). Montrer que T s'écrit : T = mg(3 cosq - 2 cosq0). Ec =mg L (cos q - cos q0 ) = ½mv2 ; v2 / L = 2g (cos q - cos q0 ). Or T= m[ v2/L + g cos q ] d'où T = 2mg (cos q - cos q0 ) + mg cos q . T = mg(3 cosq - 2 cosq0).
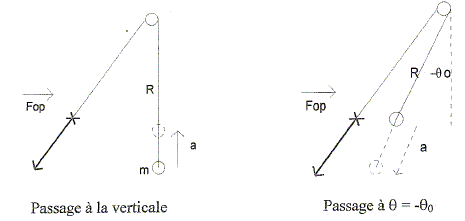
Une poulie placée en O permet à un opérateur de modifier la longueur du pendule. La force exercée par l'opérateur est égale à la tension du fil T = Fop. Lors de la première oscillation on pourra utiliser l'expression de la tension trouvée ci-dessus. Au premier passage à la verticale, la longueur du pendule est réduite de a ( a faible devant L)
|
|||||||
|
|
|||||||
|
|
 Poids
et tension du fil T.
Poids
et tension du fil T.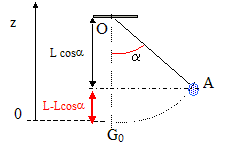 EM=
mg L (1-cos q0
).
EM=
mg L (1-cos q0
).