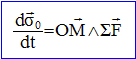Pendule de Pohl: oscillations libres amorties concours physique ITPE 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

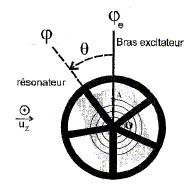
Un pendule de Pohl est constitué : - D'un disque en rotation autour de son centre. - D'un ressort spiral, qui exerce un couple mécanique qui tend à ramener le disque vers sa position d'équilibre. - D'un pointeur placé sur le disque qui permet de repérer les écarts angulaires. - D'un moteur, relié au ressort spiral, qui forcer les oscillations à une fréquence ajustable par l'utilisateur. - D'un frein électromagnétique, permettant de régler l'effet d'amortissement (par courants de Foucault). La position du disque résonateur est repéré par l'angle j(t). Le ressort spiral a une extrémité soudée en O, point fixe., l'autre extrémité mobile soudée en A au bras excitateur de position je. Le bras excitateur peut être mis en mouvement sinusoïdal de fréquence f par un moteur pas-à-pas avec une bielle. - Si je = cste, régime libre. Le moteur est étteint. - Si je = Fe cos (wt), régime forcé. Le moteur est en rotation à la fréquence f. Le disque résonateur passe dans l'entrefer d'un système magnétique alimenté par une intensité I : une force de freinage dite de Foucault est induite sur le disque résonateur. Mise en équation. Les grandeurs écrites en gras et en bleu sont des vecteurs. Le moment cinétique du disque résonateur est L=s0 =Jj' uz où J est une constante. Quelle est l'unité du moment d'inertie J ? kg m2. Le moment de la force de rappel est -Cq uz où C est une constante. Le moment de la force de freinage est -kj' uz où k = k0+lI2 avec k0 et l constantes. Comment peut-on justifier techniquement la présence du terme k0 ? Les forces de freinage sont dues au frottement mécanique ( terme k0) et aux forces de Laplace ( courants de Foucault, terme lI2) Démontrer que l'équation de la position du disque peut se mettre sous la forme : j'' + 2 xw0j' +w02j = w02je. Enoncé du théorème du moment cinétique appliqué à un point matériel : Le référentiel d'étude étant galiléen : La dérivée par rapport au temps du moment cinétique du point matériel M par rapport au point fixe O est égal au moment, par rapport à ce point, de la somme vectorielle des forces agissant sur le point matériel M . Jj'' = -kj' -Cq avec q = j -je. Jj'' + kj' +C( j -je) =0 ; Jj'' + kj' +Cj =Cje ; j'' + k/ Jj' +C/ Jj =C/ Jje. On pose w02 = C/ J et k/ J = 2 xw0 ; x = k/(2 C½J½) d'où : j'' + 2 xw0j' +w02j = w02je.(1) Quel est l'unité de x ? Chaque terme de l'équation (1) a la dimension T-2, inverse du carré d'un temps. Dimension de j' : T-1 ; dimension de w0 : T-1 ; en conséquence x est sans dimension. Le terme xw0 correspond à l'amortissement. Etude du régime libre sans freinage de Foucault. Le moteur pas à pas est éteint. La bielle est réglée pour je =0. On écarte le système de cette position et on le lâche. On enregistre j (t) en degré pour un régime pseudo-périodique. Ecrire la solution j(t) en fonction de w0 et x= x0 sans chercher à calculer les constantes d'intégration. j'' + 2 x0w0j' +w02j = 0. (2) Equation caractéristique : r2+2 x0w0 r +w02 =0 ; discriminant D = (2 x0w0)2-4w02= 4w02( x02 -1) Ce discriminant est négatif dans le cas d'un régime pseudo-périodique. j(t) = A exp(-x0w0 t) cos ( w0t+B) avec A et B des constantes d'intégration. Exprimer la pseudo-période T uniquement en fonction de w0 et x0. pulsation w = w0( 1- x02)½ ; T = 2 p/ w = 2 p / [ w0( 1- x02)½]. On définit le décrément logarithmique d = 1/n ln [j(t) / j(t+nT)] avec n entier positif. Exprimer d en fonction uniquement de x0. cos ( w0t+B) = cos ( w0(t + nT)+B) ; j(t) = A exp(-x0w0 t) cos ( w0t+B) j(t+nT) = A exp[-x0w0 (t+nT)] cos ( w0(t + nT)+B) ; j(t) / j(t+nT) = exp(-x0w0 t) / exp[-x0w0 (t+nT)] = exp[-x0w0 t + x0w0 (t+nT)] =exp(x0w0nT) d =x0w0T = x0w0 2 p / [ w0( 1- x02)½] = x02 p /( 1- x02)½. Quelles sont les conditions de validité de la formule : d ~2 px0 ? Si x02 <<1, ( 1- x02)-½ ~1+ x0 et d ~x02 p (1+ x0) ~2 px0. Cela correspond à un amortissement assez faible. 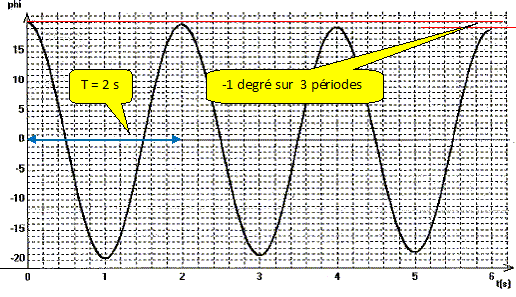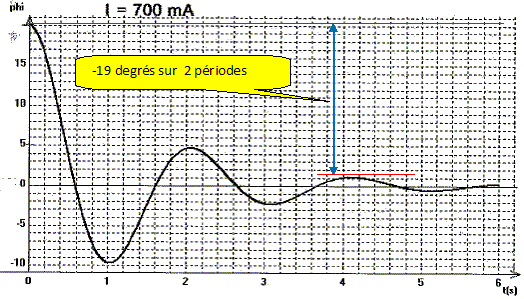Mesurer la valeur de d pour avoir la plus grande précision possible sur l'enregistrement suivant : d = 1/3 ln (20/19) ; d = 0,017 ; d ~2 px0 ; x0 =d/(2 p) =0,017/6,28 ; x0 = 2,7 10-3. Fréquence propre : 1/T0 = 1/2 = 0,5 Hz. Etude en régime libre avec freinage de Foucault.  On effectue la même expérience avec une intensité dans les bobines. I = 400 mA ; déduire la valeur de x de la courbe. d = 1/3 ln (20/5) ; d = 0,46 ; d ~2 px0 ; x400 =d/(2 p) =0,46/6,28 ; x400 = 7,4 10-2. I = 700 mA ; déduire la valeur de x de la courbe.   d = 1/2 ln (20/1) ; d = 1,5 ; d ~x02 p /( 1- x02)½ ; d2 =x02 4 p2 /( 1- x02) ; d2 ( 1- x02) =x02 4 p2 . 2,25 -2,25 x02 =39,5 x02 ; x02 = 5,4 10-2 ; x700 = 0,23. 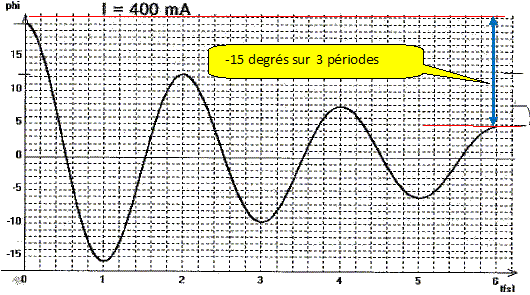Sachant que x =x0+ µI2, en déduire la valeur de µ. x0 = 2,7 10-3 ; µ = (x -x0) / I2 = (7,4 10-2 - 2,7 10-3) / 0,42 =0,44 A-2. µ = (x -x0) / I2 = (0,23 - 2,7 10-3) / 0,72 =0,46 A-2. Valeur moyenne : µ = 0,45 A-2. A partir de quelle valeur de I aura t-on un amortissement suffisant pour avoir un retour du disque à sa position d'équilibre sans dépassement ? Régime critique : x = 1 et I ~1 /µ½ =1/0,45½ =1,5 A.

retour -menu