|
Détecteur d'un spectrographe de masse physique concours DGCCRF 08
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
Un spectromètre de masse peut se décomposer en quatre parties :
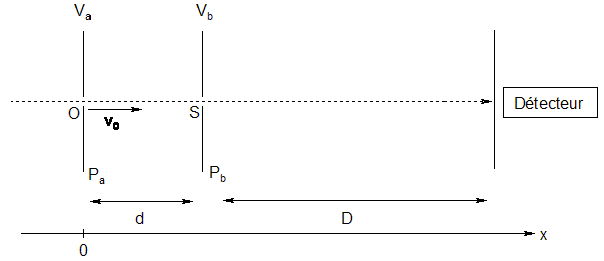
Une fois l'échantillon à analyser injecté, il est ionisé (plusieurs méthodes existent, mais elles ne seront pas développées ici), puis ces ions sont séparés dans l'analyseur (ce qui sera le sujet du problème suivant) avant d'être détectés (le signal obtenu est ensuite traité à l'aide d'un ordinateur). Mouvement d'une particule chargée dans un champ électrique. Soient deux plaques parallèles Pa et Pb, distantes d'une distance d, portées respectivement au potentiel Va et Vb. Quelle est la relation entre la tension Uab entre ces plaques et les potentiels Va et Vb ? Uab = Va -Vb. Quelle est la norme du champ électrique (notée E ) entre ces plaques ? Donner les unités de chacune de ces trois grandeurs (potentiel, tension et champ électrique). E = |Uab | / d avec Uab et Va ( volt) ; E : volt mètre -1 ; d : distance en mètre. Si un électron arrive au point O avec une vitesse v0, perpendiculaire aux plaques, à quelles forces est-il soumis ? Donner le nom et les expressions de ces forces.
- son poids, vertical, vers le bas, valeur P= mg - à une force électrique, horizontale, de sens contraire au champ électrique ( l'électron a une charge négative), de valeur F= e E. Faire un calcul d'ordre de grandeur de chacune de ces forces si on prend U = 5000 V et d = 10 cm. Conclure. Ce résultat s'applique pour toute la suite du problème. P= mg = 9,1 10-31*9,8 ~ 9 10-30 N. F = eE = eU/d =1,6 10-19 * 5000/0,1 ~ 8 10-15 N. Le poids est négligeable devant la force électrique. Pour que l'électron se dirige de O vers S, quel doit être le sens du champ électrique? Justifier. L'électron doit être accéléré entre O et S : le travail de la force électrique doit être moteur ( positif). W = q Uab = - e Uab ; Uab doit donc être négative soit Va -Vb<0 ou Vb > Va. Le champ électrique est dirigé vers le plus petit potentiel : le champ électrique est dirigé de Pb vers Pa. Dans le cas général, en appliquant la relation fondamentale de la dynamique, donner l'équation horaire du mouvement de l'électron entre O et S (équation x = f(t)). Un vecteur est écrit en gras et en bleu. F = m a ; -e E = m a ; puis projection sur l'axe Ox : eE= ma ; a = eE/m. La vitesse est une primitive de l'accélération v(t) = at+v0 ; v(t) = e/m E t + v0. La position est une primitive de la vitesse ( la position initiale est le point O) : x(t) = ½ e/m E t2 +v0t.
On considère maintenant l'analyseur à temps de vol, constitué de deux parties distinctes : celle comprise entre O et S et celle comprise entre S et le détecteur. Il n'y a aucun champ électrique entre S et le détecteur. Un laboratoire est chargé d'identifier d'éventuelles drogues dans un prélèvement sanguin. L'échantillon est préparé et injecté dans la chambre d'ionisation. Après ionisation, toutes les molécules sont monochargées (donc de charge +e) et arrivent au point O avec une vitesse négligeable. Après avoir donné l'expression de l'énergie cinétique dans le cas général, donner sa valeur pour un ion au point O. Energie cinétique d'une particule de masse m, de vitesse v en translation : Ec= ½mv2. Dans le cadre de ce problème, le théorème de l'énergie cinétique donnant la variation de l'énergie cinétique entre O et S s'exprime par : Ec(S) - Ec(O) = q.E.d. En utilisant cette relation, montrer que tous les ions de même charge ont la même énergie cinétique en arrivant au point S. E.d est une constante ; si les ions ont la même charge, q.E.d est une constante. De plus la vitesse initiale des ions est voisine de zéro, d'où : Ec(S)~q.E.d = constante. Montrer qu'en revanche, leur vitesse dépend de leur masse. Donner l'expression de cette vitesse vs. Ec(S) = ½mvs2 = q E d ; vs = (2q E d / m)½. Quel est le type du mouvement entre la plaque Pb et le détecteur ? Justifier. Le poids est négligeable ; le champ électrique est nul ( donc la force électrique est nulle). D'après le principe d'inertie ( 1ère loi de Newton ) , le mouvement d'un ion est rectiligne uniforme.
|
|||||||
|
|
|||||||
|
|