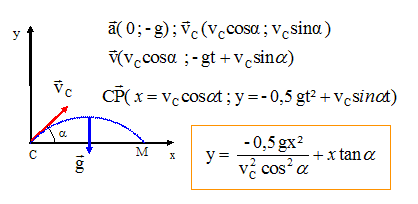Vitesse moyenne, oscillateur élastique, satellite, projectile : physique concours ESIEE 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Répondre par vrai ou faux. Un véhicule parcourt 560 km à une vitesse moyenne de 70 km.h-1. A- Le trajet dure 8 heures. Vrai. 560/70 = 8 heures B- Pour réduire le temps de trajet de 60 minutes, la vitesse moyenne doit être de 80 km.h-1. Vrai. 560/7 = 80 km h-1. C- Avec une vitesse moyenne de 75 km.h-1, le gain de temps est de 30 minutes exactement. Faux. 560 / 75 =7 ,47 heures = 7 h 28 min ; gain = 32 min. D- En roulant à 75 km.h-1 pendant la durée du trajet initial, le véhicule peut parcourir 40 km supplémentaires. Vrai. 75*8 = 600 km. E- Pour parcourir 660 km en 7 heures et 20 minutes, il faut rouler à plus de 91 km.h-1. Faux. 7 h 20 min = 7,33 h= 22/3 h. Puis 660 /22*3 =30*3 = 90 km/h. Une masse m =100 g est attachée à un ressort fixé en I. 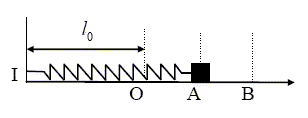Le ressort possède une longueur à vide l0 = IO =10 cm et une constante de raideur k = 40N.m-1. On note A et B deux positions de m telles que OA = a = 2 cm et OB = 2a. On note Ep él (P) l’énergie potentielle élastique en P. A-Ep él(A) =½k(l0+a)2. Faux. allongement du ressort : IA-IO = OA = a ; Ep él (A) = ½ka2. B- Ep él(B) =2 Ep él(A) . Faux. allongement du ressort : IB-IO = OB = 2a ; Ep él (B) = ½k(4a2) = 4 Ep él (A). C- Ep él(A) =8 mJ. Vrai. Ep él (A) = ½ka2=0,5*40*(2 10-2)2 =8 10-3 J = 8 mJ. D- Ep él(B) =16 mJ. Faux. Ep él (B) =4 Ep él (A) = 32 mJ. E- Ep él(O) =½kl02. Faux. Ep él(O)=0, ressort non déformé. 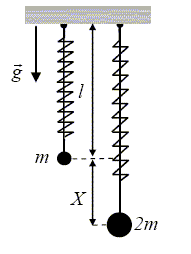Une masse m est suspendue à une extrémité d’un ressort sans masse, de constante de raideur k et de longueur à vide l0 . L’autre extrémité est fixée à un support immobile. On note l la distance du support à la masse m à l’équilibre. Une masse 2 m est suspendue à une extrémité d’un ressort de mêmes caractéristiques. On note X la distance entre les positions d’équilibre des masses m et 2m . g représente l’accélération de la pesanteur, supposée constante. On donne g =10m.s-2 ; l0 =10 cm, k =10 N.m-1 et X = 5 cm. A- m = kX/g. Vrai. A l'équilibre le poids compense la tension du ressort. mg = k(l-l0) (1) et 2mg = k(l+X-l0) (2). (2) - (1) donne : mg = kX ; m = kX/g B- m vaut 50 grammes. Vrai. m = kX/g = 10*0,05/10 = 0,05 kg = 50 g. C- l = l0 + ½X. Faux. (2) + (1) donne : 3mg = k(2l-2l0+X) avec mg = kX. 3kX = k(2l-2l0+X) ; 3X = 2l-2l0+X ; X = l-l0. D- l = 15 cm. Vrai. l = l0+X = 10+5 = 15 cm. E- La tension du ressort subie par la masse m a pour expression -kl. Faux. 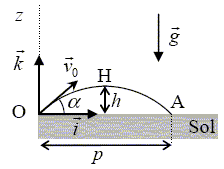valeur de la tension T = k(l-l0) S est un satellite stationnaire d’une planète P : il reste en permanence à la verticale d’un même point de la surface de la planète P. On donne la constante de gravitation universelle G = (20 / 3).10-11 SI la masse de P : 1020 kg ; le rayon de P : 100 km ; la durée d’un jour sidéral de P : 10 heures. A- La période de révolution de S autour de P est de 10 heures. Vrai. B- La vitesse de S est de l’ordre de 100 m/s. Vrai. v= [GM/(R+h)]½ ; 2 pi ( R+h) = v T ; T2/(R+h)3 = 4 pi2/(GM) 3è loi de Kepler. 4 pi2/(GM) ~ 4*10*3/(20 10-11* 1020) =6 10-9 ; T2 = (3,6 104)2 ; (R+h)3 = (36 103)2 /(6 10-9 )= 63 * 1015 ; R+h = 6 105 m = 600 km. v= [GM/(R+h)]½ =[20 10-11* 1020/(3*6 105)]½ = [20 109/(18 105)]½ =[20/18 104]½ ~ 100 m/s C- S évolue à une altitude de 36000 km. Faux. R+h = 600 km ; h = 500 km. D- L’accélération de S est nulle. Faux. l'accélération est centripète : a = v2/(R+h)~ 104 /6 105 =0,1/6 ~0,017 m s-2. E- Le champ de pesanteur au niveau du sol de P vaut (2 /3) m.s-2. Vrai. g0 = GM/R2 = 20 10-11* 1020/(3*1010) =2/3 m s-2. A t = 0 et à partir de O, on lance une bille de masse m, supposée ponctuelle, avec une vitesse v0 faisant un angle a avec l’axe horizontal. On note p = OA la portée, h la hauteur maximale atteinte par le projectile et H le point de la trajectoire correspondant à cette hauteur. On néglige tout frottement. On donne a = 30° ; v0 = 6 m/s ; g = 10 m s-2 ; m = 200 g. A- p = 1,8 *3½ m . Vrai. p = v0 cos a t ; t = p /( v0 cos a) repport dans l'expression de y(t) : 0 = -0,5 g p2/(v0 cos a)2+ p tan a. simplifier par p / cos a : 0 = -0,5 g p/(v02 cos a)+ sin a. p = 2v02 cos a sin a / g = v02 sin (2a )/ g. p = 36 sin 60 / 10 = 3,6*3½ /2 = 1,8 *3½ m B- h = 0,9 *3½ m . Faux. En H la composante verticale de la vitesse est nulle : -gt +v0 sin a= 0 ; t = v0 sin a/ g. repport dans l'expression de y(t) : h = -0,5 (v0 sin a)2/g + (v0 sin a)2/g = (v0 sin a)2/(2g). h = (6*sin 30)2 / 20 =9/20 = 0,45 m. C- La vitesse de m en H est nulle. Faux. En H la composante verticale de la vitesse est nulle ; la composante horizontale n'est pas nulle. D- L’accélération de m en H est nulle. Faux. l'accélération a pour composante ( 0 ; -g). E- H est atteint à l’instant t = 0,3 s. Vrai. t = v0 sin a/ g = 6*sin 30/10 = 0,3 s.

retour -menu