|
Oscillateur mécanique, : physique concours ECE 08
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||
| .
. |
||||||
|
||||||
|
Répondre par vrai ou faux. Soit un oscillateur mécanique vertical formé d’un ressort de constante de raideur k, de longueur l = 1 m à l'extrémité duquel on a attaché une masse m. Lorsque l'on suspend une masse m=100 g à l'extrémité libre du ressort celui-ci s'allonge de Dz == 2 cm. On prendra g=10 m.s-2 et pi2 = 10. libre du ressort celui-ci s'allonge de A- La constante de raideur du ressort a pour valeur k= 5 N.m-1. Faux. A l'équilibre, la tension du ressort est égal au poids de la masse accrochée au ressort. kDz = mg ; k = 0,1*10/0,02 =1/0,02 = 50 N m-1. B- L'expression de la période propre de cet oscillateur est d’environ 1,4 s. Faux. T = 2 pi (m/k)½ =2 pi (0,1/50)½ = 2 pi (2 10-3)½ ; T2 = 4 pi2 * 2 10-3 =2*4*10-2 ; T = 1,4*2*0,1 = 0,28 s. L’oscillateur est placé maintenant en position horizontale. Un piston, attaché à son extrémité provoque des ondes de compression et de dilatation. La position du piston évolue de façon sinusoïdale, avec une période T=0,1 s et une amplitude de 1cm. La célérité des ondes le long du ressort est de v= 2 m/s. C- La spire située au milieu du ressort commence à osciller avec un retard de 0,25 s. Vrai. Distance de cette spire à la source : 0,5 m ; cette spire reproduit le mouvement de la source avec un retard de 0,5/2 = 0,25 s. D- La source et la spire du milieu sont en opposition de phase. Vrai. fréquence f = 1/T = 1/0,1 = 10 Hz ; longueur d'onde l = c/f =2 /10 = 0,2 m Distance de la source à la spire du centre : 0,5 m soit 2,5 longueurs d'onde. Deux points distants d'un nombe impair de demi longueur d'onde vibrent en opposition de phase.
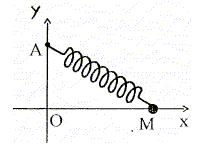
Ce ressort est enfilé sur une tige horizontale. L'une de ses extrémités P est fixe et l'autre est attachée à un solide S1 de masse M=150 g pouvant coulisser sans frottement sur l'axe. Au repos le centre d'inertie G de S1 est en O. Un solide S2 de masse m=50 g se déplaçant sans frottement sur l'axe dans le sens xx' avec une vitesse v0 = 2 m/s heurte S1 au repos en O. Après le choc, S2 reste accroché à S1. Le système oscille alors sans amortissement autour de 0 avec une amplitude xm =10 cm. La vitesse du système (S1+S2) immédiatement après le choc est v= 0,5 m/s . On donne les valeurs de calculs suivantes : 2 pi = 6,28 ; 1/12,56 = 0,08 ; 0,00748½ = 0,087. Energie cinétique avant le choc : ½
mv02 = 0,5*0,05 *4 =0,1
J. Energie cinétique après le choc :
½ (m+M)v2 = 0,5*0,2
*0,52 =0,025 J. Energie perdue au cours du choc : 0,1-0,025 =
0,075 J. Conservation de l'énergie mécanique : ½kxm2 = ½(M+m)v2max. k *0,12 = 0,2 *0,52 ; k = 5 N/m. C- La période d’oscillation de l'oscillateur formé par le ressort, S1et S2 est T= 1,256 s. Vrai. T = 2 pi ((m+M)/k)½ =2 pi (0,2/5)½ = 2 pi *0,04½ =2 pi *0,2 = 6,28*0,2 = 1,256 s. En fait S2 ne reste accroché à S1 que pendant la première phase de compression, S2 repart ensuite dans le sens opposé et se sépare de S1 avec une vitesse v2 = 0,5 m.s quand il repasse par la position de repos en 0. D- l'amplitude du nouvel oscillateur (ressort et S1) est xm =0,087 m. Vrai. Conservation de l'énergie mécanique : ½kxm2 = ½Mv2max. 5 xm2 =0,15 *0,52 ; xm2 =0,03*0,25 =0,0075 ; xm = 0,087 m
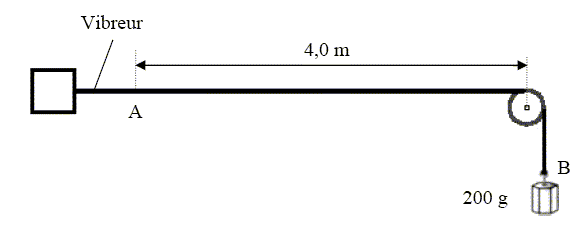
On attache une masse de 200 g à l’extrémité B d'une corde maintenue horizontale sur sa plus grande longueur, puis on produit une déformation sinusoïdale, de fréquence 100 Hz, à l’extrémité A de la corde, grâce à un vibreur. La célérité des ondes le long de la corde est donnée par la relation : v = (T/m)½. T est la tension de la corde et m= 20 g m-1, la masse linéique de la corde. On prendra : g = 10 N.kg-1 et on admettra que la valeur de la tension de la corde est égale au poids de la masse suspendue.
A- La tension peut s’exprimer en kg.m.s-1. Faux. force = masse * accélération = masse *longueur / temps2 ; [tension] =M L T-2. B- La célérité de l’onde augmente avec la masse linéique de la corde. Faux. v = (T/m)½ ; la célérité diminue si la masse linéique augmente. C- La corde est le siège d’oscillations forcées. Vrai. Une corde tendue entre deux points fixes et soumise à une excitation sinusoïdale entre en résonance lorsque les fréquences excitatrices sont multiples d'une même fréquence f0, appelé mode fondamental. On peut observer la formation d'ondes stationaires. D- La valeur de la longueur d’onde est l =10 cm. Vrai. T = mg = 0,2*10 = 2 N ; m = 20 g m-1 = 0,020 kg m-1 ; v = [2/0,02]½ =10 m/s. f = 100 Hz ; l =v /f = 10 / 100 = 0,10 m = 10 cm.
|
||||||
|
|
||||||
|
|