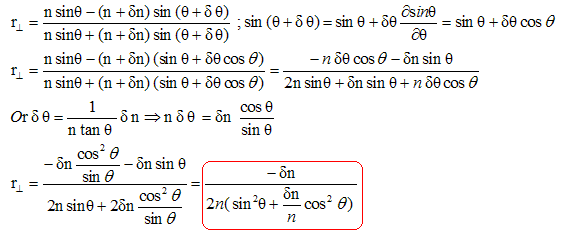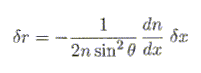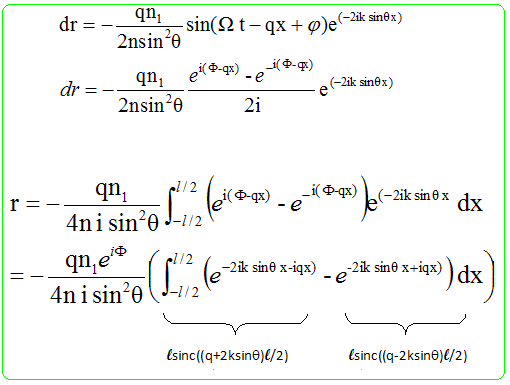|
interaction d'une onde électromagnétique avec une onde sonore concours physique agrégation 2008.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||
| .
. |
|||||||||||
|
|||||||||||
|
Le milieu diélectrique est parcouru par une onde sonore qui modifie la densité d'atomes et entraîne donc une modification de l'indice du milieu : n(r,t) = n0 +n1(r,t). On note W : pulsation de l'onde sonore ; w >> W : pulsation de l'onde électromagnétique. On pourra donc en général considérer que le motif n(r) du à la présence de l'onde sonore est figé pendant que l'onde électromagnétique le traverse.
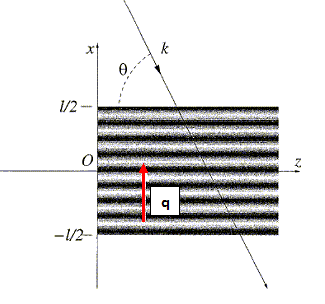
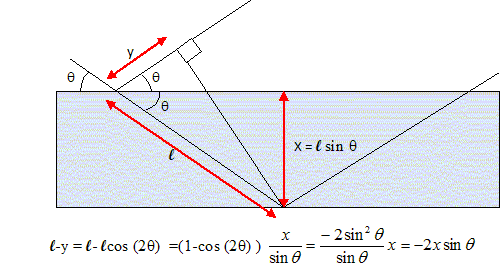
Interaction d'une onde lumineuse avec une onde sonore : k est le vecteur d'onde de la lumière et q celui de l'onde sonore de longueur d'onde L. Régime de Bragg : On considère une tranche du milieu diélectrique d'épaisseur l dans la direction Ox traversé par une onde lumineuse de pulsation w de longueur d'onde dans le milieu l et donc de vecteur d'onde dans le milieu k = nw /l ek, et dans laquelle se propage aussi une onde sonore dans la direction Ox. On appellera W la pulsation de l'onde sonore et L sa longueur d'onde. On introduira le vecteur d'onde correspondant q = nW /L ex. n1(r,t) = n1 cos (Wt-qx+j). On pourra prendre lorsque cela sera utile une onde sonore de fréquence 80 MHz et une onde lumineuse de longueur d'onde dans le vide 532 nm. Pour décrire cette situation, nous allons considérer en fait le milieu comme une succession continue de dioptres représentant la variation d'indice dans la direction x. Chacun de ces dioptres élémentaires réfléchit une partie de l'onde lumineuse incidente, et l'addition de toutes ces ondes élémentaires représentera une onde lumineuse réfléchie par l'onde sonore. réflexion d'une onde lumineuse par un
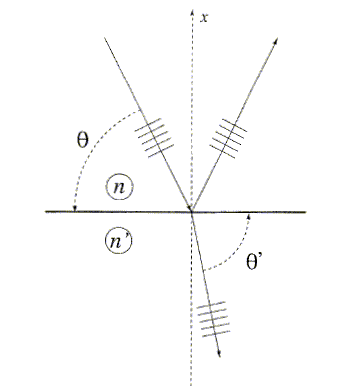
dioptre : les angles ne sont pas définis
selon la convention habituelle. on note n et n' les indices de réfraction des deux milieux homogènes. Rappeler les lois de Descartes relatives à la réflexion et à la réfraction par le dioptre. Le rayon incident et le rayon réfléchi sont coplanaires ; l'angle de réflexion a même mesure que l'angle d'incidence ; le rayon traverse la normale à la surface. Le rayon réfracté et le rayon incident sont coplanaires ; le rayon réfracté traverse la normale à la surface ; on note i ( angle d'incidence) et i' ( angle de réfraction) les angles définis entre les rayons et la normale. n sin i = n' sin i'soit avec la figure ci-dessus : n cos q = n' cos q '. On appelle les expressions de Fresnel donnant les coefficients de réflexion en amplitude pour une onde d'incidence q ( on note q ' l'angle d'émergence) défini sur la figure :
En conséquence la lumière réfléhie par un dioptre est généralement polarisée : - on diminue les reflets sur une photo en utilisant un filtre polarisant - le coefficient de reflexion parallèle peut s'annuler : diminution des pertes dans les systèmes optiques utilisant des lasers. Enfin si n > n' et cos q = n'/n, il y a réflexion totale ( absence de rayon réfracté) : alors les coefficients de réflexion valent 1. Réflexion par un faible saut d'indice : On se place dans le cas particulier où la différence d'indice de part et d'autre du dioptre est très faible. On note n l'indice d'un côté et n+dn l'indice de l'autre côté du dioptre. De même on note q ' = q +dq. La loi de Descartes pour la réfraction s'écrit : n cos q = (n+dn) cos (q +dq). Développer et ne conserver que les termes au premier ordre :
Expression des coefficients de réflexion :
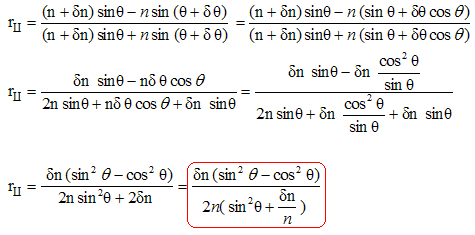
Sous incidence rasante q tend vers zéro et cos q tend vers 1. Les deux coefficients sont identiques : l'amplitude de l'onde réfléchie ne dépend pas de la polarisation. d r ~ -dn / (2n sin2q) Réflexion par une variation d'indice. On suppose que l'indice dépend continuellement de la cote x. Montrer qu'une tranche d'épaisseur dx
contribue à la réflexion par le coefficient :
Variation de l'indice à travers la tranche : dn = dn/dx dx. On se retrouve dans le cas où la différence d'indice de part et d'autre du dioptre est très faible. On note n l'indice d'un côté et n+dn l'indice de l'autre côté du dioptre. L'expression d r ~ -dn / (2n sin2q) s'écrit : d r ~ -1/(2n sin2q) . dn/dx .dx. Diffraction de Bragg. Calcul de dn/dx dans le cas où le milieu est traversé par l'onde sonore décrite au début. n(r,t) = n1 cos (Wt-qx+j) ; dn/dx =qn1 sin(Wt-qx+j). Dans le cas étudié ici, l'indice est partout très peu différent de sa valeur moyenne, on pourra donc considérer avec une bonne approximation que la lumière s'y propage en ligne droite. On prend comme référence de phase l'onde réfléchie par le plan de cote x=0. Phase de l'onde réfléchie par le plan de cote x :
DF = 2p/l (-2x sin q).
|
|||||||||||
|
|
|||||||||||
|
|