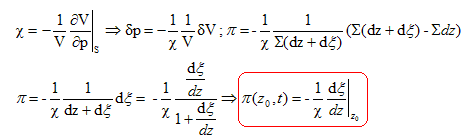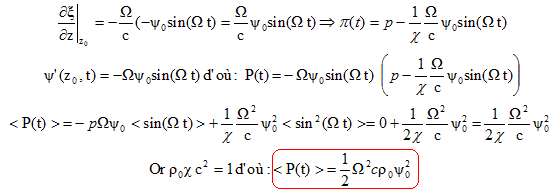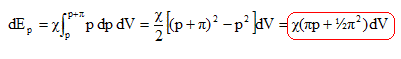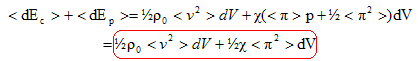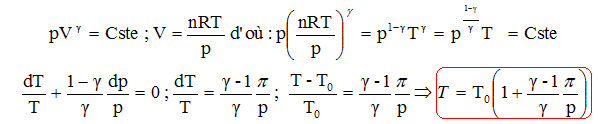les ultrasons : aspect énergétique ; densité d'énergie sonore, atténuation concours physique agrégation 2008.

. .

. .

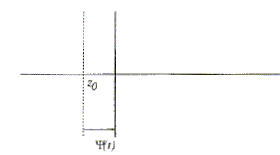
Une onde sonore transporte de l'énergie. On place dans le milieu un piston sans masse, d'extension transversale suffisamment grande pour qu'on puisse négliger les effets de bord, placé perpendiculairement à la direction de propagation d'une onde sonore, à l'abscisse z= z0. Au passage de l'onde il se déplace de Y(t). Le principe fondamental de la dynamique indique qu'un piston sans masse n'est soumis à aucune force de la part du milieu extérieur. Le principe de l'action et de la réaction indique que le piston n'exerce, en retour, aucune action sur le milieu : le piston ne perturbe donc pas l'onde. Pour décrire la déformation du milieu, on isole une tranche d'épaisseur infinitésimale dz et on écrit que cette tranche est déplacée de x(z, t). Y(t) = x(z0, t). On fait le vide à gauche du piston et un opérateur maintient le piston en position. L'opérateur imprime alors au piston un mouvement caractérisé par le même déplacement Y(t) que dans la situation précédente. - A droite du piston, rien n'a changé par rapport à la situation précédente : l'onde qui s'y propage est identique. - A gauche du piston, une onde sonore ne peut pas se propager dans le vide. Force F(t) exercée par l'opérateur, par unité de surface, pour imposer le déplacement Y(t) : Le piston étant sans masse, la force exercée par l'opérateur compense la force pressante exercée par le milieu. F(t) = p + p(z0,t). Compressibilité adiabatique c du milieu ( l'indice S signifie " à entropie constante"). La tranche d'aire S( épaisseur initiale dz et volume initial Sdz ), d'épaisseur finale dz+dx, de volume final S(dz + dx) subit une variation de pression dp = p : On peut négliger dx /dz devant 1 dans la mesure où le volume de la tranche varie peu et dans la mesure où la variation de pression p est petite devant p0. On suppose que le déplacement du piston est sinusoïdal de pulsation W : Y(t) = Y 0 cos (Wt). Puissance mécanique moyenne P dépensée par l'opérateur, par unité de surface pendant une période de l'onde : Puissance instantanée P(t) = Y ' (t) . F(t) Or Y(t) = x(z0, t) , soit x(z, t) = Y 0 cos [W (t- (z-z0) / c)]. Puissance moyenne déployée par l'opérateur pour imprimer un mouvement quelconque au piston : On suppose que le déplacement est la somme de deux fonctions sinusoïdales de pulsation W1 et W2. Déplacement : x1 + x2 ; surpression p1 + p2 ; la valeur moyenne d'un sinus étant nulle, <P> = <P1> +<P2> . Tout mouvement peut être décomposé en somme de fonctions sinus de pulsation yn par la transformée de Fourier.   Densité d'énergie sonore. Considérons un élément de volume dV du milieu d'extension petite devant la longueur d'onde de la perturbation sonore. Lors du passage de l'onde, cet élément de volume est comprimé ( ou déprimé) et mis en mouvement. Masse dm de set élément : dm = r0 dV. On note v sa vitesse. Energie cinétique de cet élément : dEc = ½dm v2 = ½r0 v2 dV. Energie potentielle de compression ou travail reçu lorsque la pression varie de p à p +p : Travail élémentaire : d2W = -pd2V. Dans le cas d'une transformation adiabatique : d2V = c dp dV. 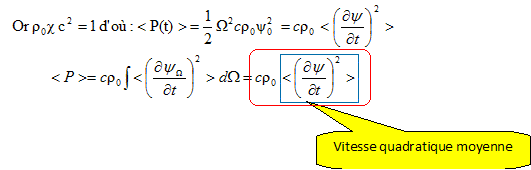En conséquence : d2W = -c p dp dV puis intégrer de p à p+p : L'énergie interne moyenne augmente lors du passage de l'onde de : (en tenant compte du fait que <p>=0 ) Pour une onde sinusoïdale : p (z, t) = -1/c dx/dz avec x(z, t) = Y 0 cos [W (t- (z-z0) / c)]. dx/dz = Y 0W / c sin [W (t- (z-z0) / c)]. p (z, t) = -Y 0W / (c c) sin [W (t- (z-z0) / c)] vitesse v (z, t)= dx/dt = -Y 0W sin [W (t- (z-z0) / c)] = p (z, t) c c. Soit en valeur quadratique moyenne : <v2(z, t)> = < p 2 (z, t) > c2 c2 . Densité d'énergie sonore : <v2(z, t)> / (2cc2) + ½r0 <v2(z, t)> . Or r0c c2 = 1 d'où la densité d'énergie sonore : r0 <v2(z, t)> =c< p 2 (z, t) >. Atténuation du son.  Lors du passage de l'onde acoustique une tranche du milieu subit une alternance de phases de compression et de détente. Cette alternance conduit à une variation alternative de la température de la tranche. On se place dans le cadre de l'approximation acoustique : le volume de la tranche varie peu et la variation de pression p est petite devant p0. On pourra remplacer les variations de pression et de température par leurs différentielles. Que devient l'énergie d'une onde lors de son atténuation ? L'énergie mécanique est convertie en énergie interne : la température du milieu va donc augmenter. Dans un gaz parfait la température dépend de la pression : équation des gaz parfaits : pV = nRT Pour une transformation adiabatique : si la variation de pression p est positive, la température s'élève. Atténuation de l'onde : La conduction de la chaleur est supposée régie par la loi de Fourier : ( D est le coefficient de diffusion thermique). Cette équation décrit un phénomène irréversible ; la chaleur va naturellement du chaud vers le froid. Prenons le cas d'une onde sinusoïdale, de longueur d'onde l. A un instant donné, la température est alors une fonction sinusoïdale de l'abscisse, de ptériode spatiale l : T(z) = T0 + T1 cos ( 2pz / l + F ). Expression du courant thermique associé : Le courant thermique est d'autant plus grand que la longueur d'onde l est plus petite (fréquence élevée). Les ondes de haute fréquence seront atténuées plus rapidement.

retour -menu