|
Lunette afocale, arc en ciel, concours Caplp maths sciences 2009.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
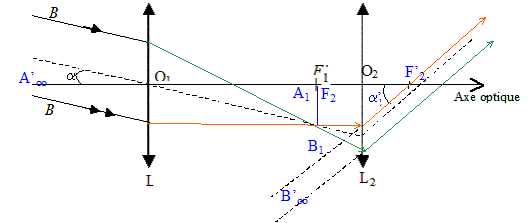
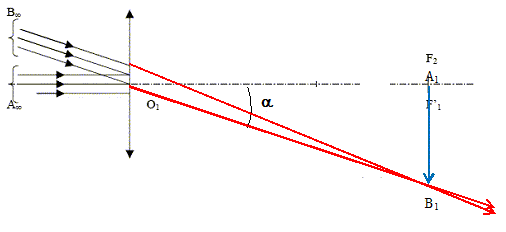
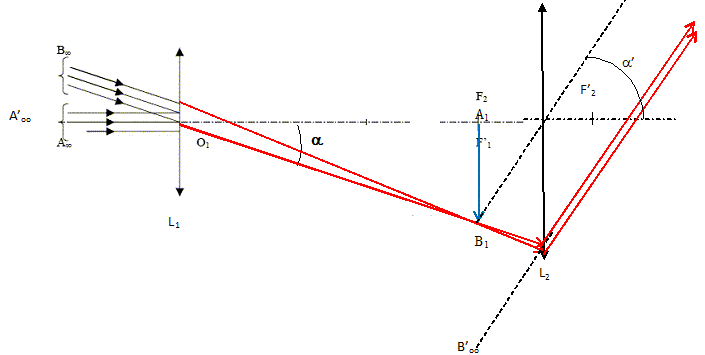
On considère un télescope assimilable à l'association d'une lunette astronomique dont l'objectif est une lentille convergente L1 de centre optique O1, de distance focale image f1 =25,0 m et de diamètre d'ouverture D, et d'un oculaire représenté par une lentille convergente L2 de centre optique O2, de distance focale image f2 =2,50 cm. On observe un objet à l'infini ( une étoile). L2 est disposée de telle façon que l'ensemble ( objectif + oculaire) donne de l'objet à l'infini une image à l'infini. Quel est l'intérêt d'un tel réglage pour l'oeil de l'observateur ? L'oeil observe sans accommoder, sans fatigue. Déterminer O1O2 et placer L2, O2, les foyers principaux ( objet et image) de L1 et L2. Le foyer image de L1 est confondu avec le foyer objet de L2 : O1O2 = f1+f2 = 25 +0,025 = 25,025 ~25,0 m.
On observe avec ce télescope une étoile-double assimilable à deux sources ponctuelles Aoo et Boo, d'écart angulaire a tel que |a|=3,8 10-5 rad. ( étoile-double Sirius de la constellation du "Gtand chien") Compléter le tracé de chaque rayon au delà de L1 et L2.
A1 et B1, points images de Aoo et Boo sont dans le plan focal image de L1, dans le plan focal objet de L2. Déterminer la distance A1B1 en fonction de a et f1. A1B1 ~ a f1 = 3,8 10-5 *25,0 =9,5 10-4 m.
a' ~ A1B1/f2 = 9,5 10-4 / 0,025 =3,8 10-2 rad. Ga = a' / a = f1/f2 =25 / 0,025 =1000. L'oeil ne peut pas distinguer les détails dont l'écart angulaire est inférieur à une valeur limite a lim = 3 10-4 rad. Les deux composantes de Sirius sont-elles séparées par l'oeil nu ? Par l'oeil placé derrière l'oculaire du télescope ? a < a lim : l'oeil nu ne distingue pas l'étoile-double. a'> a lim : l'oeil derrière le télescope distingue l'étoile-double. L'ensemble oculaire + oeil est mlaintenant templacé par un capteur de lumière disposé dans le plan focal image de L1. Pour simplifier, on suppose que sa capacité à distinguer les détails est , contrairement à l'oeil, illimitée. Lorsqu'on observe un ciel étoilé, on constate que les étoiles scintillent. A quoi est du ce phénomène ? Les étoiles très éloignées de la terre sont ponctuelles pour l'observateur terrestre. Le scintillement est du aux réfractions multiples et aléatoires de la lumière dans les couches turbulentes de l'atmosphère terrestre. Par la suite on considèreré que la scintillation, dans les meilleurs conditions, transforme un point image en une tache circulaire dont le diamètre minimum est : dmin=1,0 10-6 f1. Dans l'étude précédente, on n'a pas tenu compte du phénomène de diffraction, qui a pour effet de remplacer la point image B1 par une tache de diffraction circulaire de centre B1 et de diamètre d1 = 1,22 l/D f1 ( de même pour B2). Pour l = 0,55µm, déterminer à quelle inégalité doit satisfaire D pour que la diffraction ne perturbe pas la formation des images davantage que ne le fait le phénomène de scintillation. d1 < dmin ; 1,22 l/D <1,0 10-6 ; D >1,22 l/1,0 10-6 ; D >1,22 *0,55 10-6 / 1,0 10-6 ; D >0,67 m. En supposant satisfaite la condition précédente, déterminer la valeur numérique de amin ( écart angulaire minimum que le télescope peut séparer). Deux images sont séparées si le centre B2 de la deuxième tache est située à l'extérieur de la première tache centrée sur B1. B1B2 = dmin = 1,0 10-6 f1 ; A1B1 ~amin f1 ; amin = 1,0 10-6 rad. Les grands télescopes employés aujourd'hui ont une ouverture de plusieurs mètres. Quelle est l'utilité d'une telle dimension ? d1 = 1,22 l/D f1 ; plus D est grand plus d1 est petit : on améliore ainsi la qualité des détails de l'image. Quel est l'intérêt d'embarquer un télescope sur un satellite artificiel autour de la terre. Leur position au dessus de l'atmosphère permet d'obtenir une qualité d'image bient supérieure à celle des télescopes terrestres. Permettre aux scientifiques de disposer d'équipements d'observation en permanence, de jour comme de nuit.
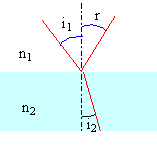
Propagation de la lumière blanche dans un milieu réfringent. On envoie un mince faisceau de lumière jaune au centre de la face plane d'un hémi-cylindre de plexiglas sous incidence i = 75 °. Enoncer les lois de Descartes pour la réfraction et la reflexion sur l'interface air-plexiglas d'indice n=n2. Les rayons incidents, réfléchi et réfracté sont dans le même plan.
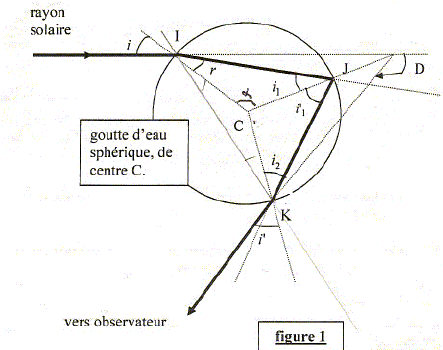
Les angles i1 ( angle d'incidence) et r ( angle de réflexion ) ont même mesure. n1 sin i1 = n2 sin i2. On fait arriver sur l'hémi-cylindre un mince faisceau de lumière blanche. On constate un étalement spectral de la lumière réfractée. Comment nomme t-on ce phénomène ? Comment l'explique t-on ? Dispersion de la lumière blanche par le plexiglas La célérité de la lumière dans le plexiglas dépend de la fréquence. Arc en ciel primaire. l'arc en ciel résulte de réfractions et réflexion(s) de la lumière dans les gouttes d'eau en suspension dans l'air. Les gouttes sont supposées sphériques. On note n(l) l'indice de l'eau associée à une lumière monochromatique de longueur l dans le vide et la valeur de l'indice de l'air sera prise égale à 1,000. On étudie la marche d'un rayon monochromatique de longueur d'onde l.
Quel est l'angle formé par les droites (CI), (CJ) et CK) avec l'interface air-eau ? Ces trois droites correspondent aux rayons du cercle de centre C : elles sont perpendiculaires à l'interface air-eau. Le repèrage angulaire proposé est-il pertinent pour l'application des lois de Descartes ? Les angles i, r, i1,i2 et i' sont repèrés par rapport à la normale à l'interface : c'est donc pertinent. Donner les relations liant i1, i2 à r. i1 = i2 : le triangle CJK est isocèle ; r = i1 : le triangle CJI est isocèle. r = i1 =i2. Quelles est la relation entre i et r ? entre i' et i ? réfraction en I : sin i = n(l) sin r = n(l) sini2 ; réfraction en K : n(l) sin i2 = sin i' ; d'où i = i'. Montrer que la déviation D du rayon vérifie : D = 180+2i-4r. Réfraction en I : déviation i-r ; réflexion en J : déviation 180 - 2i1 = 180 -2r. Réfraction en K : déviation i'- i2 = i-r ; d'où D = i-r +180-2r + i-r = 180 + 2i -4r.
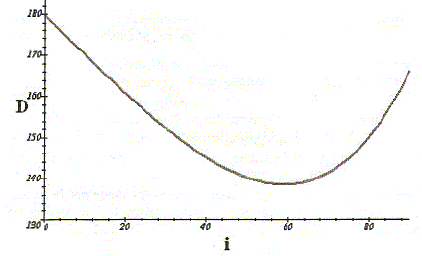
La variation de D en fonction de i est donnée pour une des longueurs d'onde du visible :
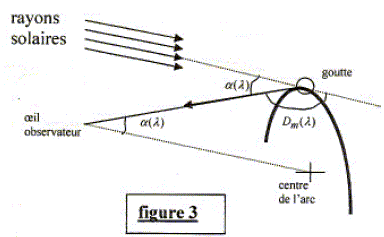
A l'aide de cette courbe, expliquer pourquoi on peut parler d'accumulation de lumière pour D voisin d'une valeur Dm(l) dont on déterminera la valeur ? Quelle est la valeur im(l) associée ? Au voisinage du minimum de déviation, la déviation dépend peu de l’angle d’incidence : il en résulte une concentration des rayons émergents autour de la direction de déviation minimum et en conséquence l’intensité lumineuse est maximale dans cette direction. Dm(l) ~ 140 ° et im(l) ~ 60°. On démontre que im(l) obéit à l'équation : sin2(im(l) ~) = 1/3 (4-n2(l)). Du fait de l'accumulation de lumière constatée au voisinage de Dm(l), on considérera désormais que seule l'incidence im(l) contribue à l'observation de l'arc en ciel. On considère maintenant deux longueurs d'onde l1 et l2 ( correspondant à deux couleurs de l'arc en ciel) pour lesquelles l'indice de l'eau vaut respectivement 1,330 et 1,344. On admet la loi de Cauchy selon laquelle n(l) = n0 + C/l2 où n0 et C sont deux constantes positives. En déduire laquelle de ces deux longueurs d'onde est la plus proche de la limite rouge du spectre de la lumière visible. n(l) est d'autant plus grand que l est plus petit. 1,344 correspond donc à la plus petite longueur d'onde ; 1,330 correspond à la plus grande longueur d'onde ; Les longueurs d'onde de la lumière visible sont comprise entre 0,4 µm ( limite du bleu) et 0,8µm ( limite du rouge). l1 est la plus proche de la limite de la lumière rouge.
Pour l1 : sin2(im(l) )~ =1/3( 4-1,332) = 0,744 ; im(l) =59,58 ° ; pour l2 : sin2(im(l) )~ =1/3( 4-1,3442) = 0,731 ; im(l) =58,77 °. sin i = n(l) sin r ; sin r = sin i /= n(l) Pour l1 : sin r = sin 59,58 / 1,330 = 0,648 ; r = 40,42° ; Pour l2 : sin r = sin 58,77 / 1,344 = 0,636 ; r = 39,51°. Dm =180 + 2im -4rm. Pour l1 : Dm =180 +2*59,58-4*40,42 =137,48° ; Pour l1 : Dm =180 +2*58,77-4*39,51 =139,5° ;
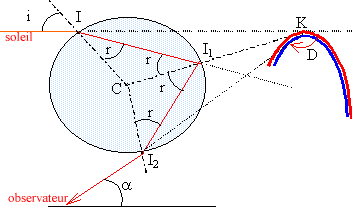
Justifier l'appellation "arc en ciel primaire à 42 °". L'arc primaire apparaît pour a (l) voisin de 42°. Un second arc-en-ciel, moins lumineux, peut être aperçu au-dessus de l'arc primaire. Il est la conséquence d'une double réflexion de la lumière du soleil à l'intérieur des gouttes de pluie. Décrire l'aspect de l'arc en ciel primaire. L'arc-en-ciel contient une infinité de couleurs. Le spectre lumineux, dont la décomposition est entraînée par la réfraction, est continu.
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|