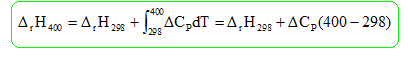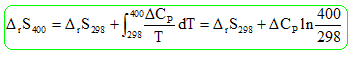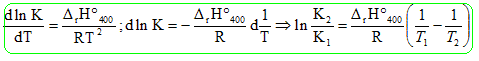étude thermodynamique de la synthèse de l'éthanol concours chimie Capes 2007. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

On fait réagir en phase gazeuse de l'éthylène avec de la vapeur d'eau pour produire l'éthanol. Cette réaction conduit à un état d'équilibre. C2H4(g) + H2O(g) = C2H5OH(g). La constante d'équilibre associée à cette réaction est notée K0. Etat standard : L'état standard correspond au corps pur dans son état physique le plus stable à la température T, sous la pression standard : p0 = 1 bar = 105 Pa. Variance du système : La variance est le nombre de paramètres intensifs indépendants. La règle des phases donne la variance d'un système thermodynamique : v = c+2-j. Le chiffre 2 indique le nombre de paramètres intensifs, température et pression. c : nombre de constituants indépendants ( nombre de constituants - nombre de réactions chimiques indépendantes entre ces constituants) Nombre de constituants : c=3 ; nombre de relation : 1 ; nombre de phase : j=1, une seule phase gazeuse. v =  c-1+2-j= 3-1+2-1 =3. Ceci signifie que la connaissance de trois paramètres suffit à connaître les proportions de l'équilibre. On choisit dans ces facteurs, par exemple, T, P, P(H2O) Relation entre les pressions partielles des constituants et K0. K0 = PC2H5OH PC2H4 PH2O On donne les enthalpies standards de formation DrH° et les entropies molaires standards Sm° à 25 °C : C2H4(g) H2O(g) C2H5OH(g) DfH° kJ mol-1 52,5 -241,8 -235,1 Sm° J mol-1 K-1 219,6 188,8 282,7 CP J mol-1 K-1 43,6 33,6 65,4 Les capacité thermiques molaires standard isobare sont supposées indépendantes de la température. Calcul de l'enthalpie standard et l'entropie de cette réaction à T1 =400 K ? DrH°298 =DrH°(C2H5OH(g)) -DrH°(H2O(g))-DrH°(C2H4(g)) DrH°298 = -235,1 +241,8-52,5 = -45,8 kJ / mol. DCP =65,4-33,6-43,6 = -11,8 J mol-1 K-1 DrH400 = -45,8 103 - 11,8*102 = -47,0 kJ/mol. DrS°298 =DrS°(C2H5OH(g)) -DrS°(H2O(g))-DrS°(C2H4(g)) DrS°298 =282,7-188,8-219,6 = -125,7 J mol-1 K-1 DrS°400 =-125,7 -11,8 ln (400 / 298) = -129,2 J mol-1 K-1. Valeur de la constante d'équilibre à 400 K. DrG° =DrH° - TDrS° = -47,0 103 +400*129,2 = 4,67 103 J / mol. De plus DrG° =-RT ln K ; ln K = 4,67 103/(-8,314*4008) = -1,404 K = 0,246. Exprimer la constante d'équilibre K en fonction des pressions partielles et de la pression  standard P°=1 bar. K = PC2H5OH PC2H4PH2O Les pressions partielles étant celles des constituants à l'équilibre. Les réactifs sont introduits en proportions stoechiométriques. On appelle taux d'avancement a, le nombre de moles d'éthanol formé par mole d'éthylène initial. Relation entre K, a, Ptot. avancement (mol) C2H4(g) + H2O(g) =C2H5OH(g) initial 0 n n 0 à l'équilibre x n-x n-x x A l'équilibre, nombre total de mol : N=2 n-x. Fractions molaires : xC2H4 = n-x 2n-x ; xH2O = n-x 2n-x ; xC2H5OH = x 2n-x Pressions partielles : PC2H4 =Ptot n-x 2n-x ; PH2O =Ptot n-x 2n-x ; PC2H5OH =Ptot x 2n-x K = PC2H5OH PC2H4PH2O = x(2n-x) Ptot( n-x)2 = a(2-a) Ptot( 1-a)2 Calcul de a à 400 K sour Ptot = 1,00 bar. 0,246 ( 1-a)2 = a(2-a) ; 1,246 a2-2,498 a+0.246 = 0 ; a =0,104 ( 10,4 %). On veut étudier l'influence de la température sur l'équilibre précédent. Dans quel sens l'équilibre précédent est déplacé lors d'une élévation de température à pression constante, le système étant fermé. DrH400 est négatif : la réaction est exothermique. Une élévation de température favorise une réaction endothermique : l'équilibre est déplacé dans le sens indirect ( vers la gauche). On élève la température de 150 K à partir de 400 K. Déterminer la valeur de la nouvelle constante d'équilibre et la valeur du coefficient de dissociation a. On suppose que DrH400 est à peu près constant sur l'intervalle de température et on utilise la relation de Vant'Hoff : ln (K2/0,246 ) = -47 103 / 8,314 [ 1/400 -1/550] = -3,85 ; K2 = 0,246 *0,021 =5,2 10-3. Autre méthode : en refaisant le calcul ci-dessus ou trouve 5,56 10-3. Calcul de a à 550 K sour Ptot = 1,00 bar. 5,56 10-3 ( 1-a)2 = a(2-a) ; 1,0056 a2-2,0112 a+0,0056 = 0 ; a =0,028 ( 2,8%). On veut maintenant étudier l'influence de la pression totale sur l'équilibre précédent. Dans quel sens l'équilibre précédent est déplacé lors d'une augmentation de pression à température constante, le système étant fermé. A l'équilibre, nombre total de mol : N= 2n-x. Dans le sens direct, le nombre total de moles diminue : une augmentation de pression à température constante, favorise la réaction qui conduit à une diminution du nombre de moles. Une augmentation de pression, à température constante, déplace l'équilibre dans le sens direct. On considère l'équilibre à T1 = 400 K sous P1 = 1 bar. Puis on augmente la pression jusqu'à 10 bars, la température restant à 400 K. Calcul de a à 400 K sour Ptot = 10 bar. 10*0,246 ( 1-a)2 = a(2-a) ; 3,46 a2-6,92 a+2,46 = 0 ; a =0,462 ( 46,2 %). Expérimentalement on travaille à 300 °C sous une pression de 70 bars. Ces conditions sont-elles en accord avec les prévisions faites précédemment ? La température proche de 573 K est défavorable à l'équilibre, mais il faut que les espèces soient gazeuse sous une pression de 70 bars. Une pression élevée déplace l'équilibre dans le sens direct. Les conditions expérimentales sont en accord avec les prévisions faites.

retour -menu