Généralités sur les ondes ; ondes sonores ; sonar ; concours physique capes 2004. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

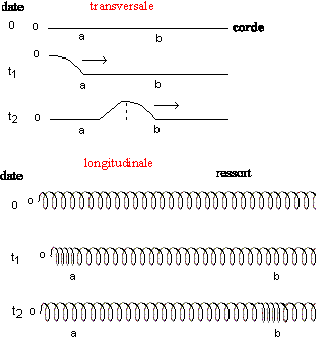
Une onde est la propagation d'une perturbation : elle produit sur son passage une variation réversible des propriétés physiques locales. Elle transporte de l'énergie, elle ne transporte pas de matière. Une onde est une région de l'espace dont les propriétés sont modifiées. Onde mécanique progressive: On appelle onde mécanique progressive le phénomène de propagation d'une perturbation dans un milieu matériel sans transport de matière, mais avec transport d'énergie. Une onde se propage, à partir de la source, dans toutes les directions qui lui sont offertes. Onde transversale, onde longitudinale : Une onde est transversale lorsque le déplacement des points du milieu de propagation s'effectue perpendiculairement à la direction de propagation. Onde transversale à la surface de l'eau : chaque point P de la surface se soulève verticalement puis reprend sa place alors que les rides se déplacent horizontalement à la surface de l'eau.   Une onde est longitudinale lorsque le déplacement des points du milieu de propagation s'effectue dans la même direction que celle de la propagation. L'onde sonore se propage dans les trois dimensions de l'espace. Chaque point P vibre longitudinalement dans la direction de propagation du signal. 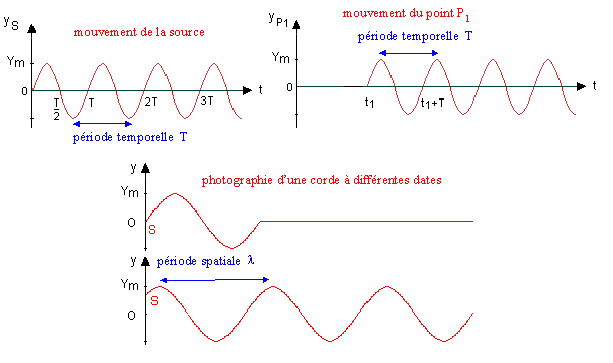Un mouvement périodique est un mouvement qui se répète à intervalles de temps égaux. La période d'un phénomène périodique est la durée au bout de laquelle le phénomène se répète identique à lui-même. On la note T et elle s'exprime en secondes (s). La fréquence d'un phénomène périodique représente le nombre de périodes par seconde. On la note généralement f, son unité est le hertz (Hz). La fréquence est l'inverse de la période. T(s) = 1/ f( Hz). Un point M du milieu, situé à la distance x (m) de la source, reproduit le mouvement de la source avec un retard t = x/v. L'onde présente une double périodicité: une périodicité temporelle de période T (exprimée en secondes). une périodicité spatiale ou longueur d'onde l (exprimée en mètres). l = v T = v / f. dispersion d'une onde : un milieu est dit dispersif si la célérité des ondes qui se propagent dans ce milieu dépend de leur fréquence - La surface de l'eau est un milieu dispersif ; - L'air est un milieu non dispersif pour les ondes sonores; - Un prisme de verre est un milieu dispersif pour la lumière. Dans quelles conditions peut-on observer des ondes stationnaires ? Soit une onde sinusoïdale se propageant, sans atténuation, sur une corde tendue entre deux points fixes distants de L. L'onde subit une réflexion sur chaque extrémité. Le phénomène est périodique de période ( durée d'un aller et retour) T0 = 2 L/v ( célérité de l'onde). Pendant cette durée l'onde s'est propagée d'une longueur 2L à la célérité v. Les deux extrémités fixes sont des noeuds de vibrations : les ondes stationnaires s'établissent si la longueur L de la corde est un multiple de la demi-longueur d'onde l. On observe au milieu de chaque fuseau un ventre de vibration d'amplitude supérieure à 2 a ( a :amplitude de la source) Qu'est-ce qu'un mode propre de vibration ? Par quelle grandeur caractérise-t-on un mode propre ? Quelle est la valeur de cette grandeur pour le mode fondamental par rapport aux modes harmoniques ? L= n ½ l ou 2L = nl avec n : nombre de fuseaux stables sur la corde de plus l = v /f soit f = n v /(2L) Les fréquences des ondes stationaires qui peuvent se propager sur une corde tendue entre deux points fixes sont les fréquences propres de vibration de la corde. Une corde tendue entre deux points fixes et soumise à une excitation sinusoïdale entre en résonance lorsque les fréquences excitatrices sont multiples d'une même fréquence f0, appelé mode fondamental. Les fréquences multiples de f0 sont appelées harmoniques. Les ondes sonores et ultrasonores. Décrire une onde sonore. Une onde sonore est une onde mécanique progressive longitudinale ( propagation d'une variation de pression) se propageant dans un milieu élastique avec transport d'énergie, sans transport de matière. Ces ondes ne se propagent pas dans le vide. Expérience : dans une chloche à vide placer une lampe et un réveil ; on réalise un vide partiel, on perçoit la lumière, on n'entend plus le son émis par le réveil. Ordre de grandeur de la bande passante de l'oreille humaine : L'oreille humaine perçoit les sons dont les fréquences sont comprises entre 20 Hz et 20 000 Hz. Un son est d'autant plus aigu que sa fréquence est plus grande ; d'autant plus grave que sa fréquence est plus petite. Placer par rapport à cette bande passante les domaines des infrasons et ultrasons. Les fréquences des infrasons sont inférieures à 20 Hz ; les fréquences des ultrasons sont supérieures à 20000 Hz Donner, à température ambiante, des ordres de grandeur de célérité pour le son dans les gaz, les liquides et les solides. dans l'air : 340 m/s ; dans un liquide ( eau de mer) : 1500 m/s ; dans l'acier : 5000 m/s. Les ondes sonores dans les gaz : La théorie cinétique de Maxwell exprime la valeur moyenne V de la vitesse des molécules d'un gaz de masse molaire M par la relation suivante : V = (8RT/(pM)½. Comparer, pour l'air à 20°C, cette valeur moyenne avec la célérité du son. Commenter le résultat. V = (8*8,31*293/(3,14 *0,029)½ = 462 m/s, supérieure à 340 m/s. L'agitation thermique est un mouvement désordonné, les molécules d'un gaz à température ordinaire se déplacent avec des vitesses de l'ordre de 4300 m/s, avec des directions aléatoires. La célérité de l'onde est la vitesse c avec laquelle l'onde se propage. Rappeler la relation du gaz parfait et les limites de ce modèle ; préciser les unités en SI. gaz constitué de particules suffisamment éloignées les unes des autres afin que leurs interactions soient très faibles, voir nulles. Dans ce cas, l’énergie potentielle d’interaction entre les molécules est négligeable devant l’énergie d’agitation thermique.( kT) Un gaz réel sous faible pression se comporte comme un gaz parfait.   PV=nRT loi des gaz parfaits P: pression du gaz en Pa V: volume du gaz en m3 n: quantité de matière de gaz en mol T: température absolue du gaz en K R: constante des gaz parfaits. R=8,32 SI On établit que la célérité c du son dans un gaz supposé parfait est donnée par la relation : c = (gRT/M))½, g étant le rapport des capacités thermiques à pression constante et à volume constant. Calculer les valeurs de c pour l'air et le dihydrogène (MH = 1 g.mol-1) à 20°C. Commenter la différence entre ces deux valeurs. cair = (1,4*8,31*293 / 0,029)½ =352 m/s ; cH2= (1,4*8,31*293 / 0,002)½ =1,3 103 m/s. La célérité du son diminue lorsque la densité du gaz augmente. Comment varie la célérité du son avec la température du milieu ? Proposer une explication de cette variation. La célérité du son dans un gaz augmente avec la température : c est proportionnele à T½. Le sonar est un système émetteur et récepteur d'ultrasons qui permet de mesurer la profondeur des océans. Un sonar est disposé sous la coque d'un navire et émet des ondes de fréquence f = 40,0 kHz, verticalement vers le fond de l'océan. Le récepteur placé à côté de l'émetteur arrête l'émission de l'onde dès la réception de l'onde réfléchie par le fond. Un compteur relié à l'émetteur permet de dénombrer le nombre n de périodes temporelles complètes émises. Le navire teste d'abord son sonar en étant à l'ancre dans un port. La profondeur de l'eau dans le port est h = 20,0 m. On réalise une mesure qui indique n = 1100. Déterminer la célérité c des ultrasons. période temporelle : 1/40000 =2,5 10-5 s ; durée de l'aller et retour de l'onde : 1100 * 2,5 10-5 =2,75 10-2 s. c = 20*2 / 2,75 10-2 ~ 1,45 103 m/s. Combien de périodes spatiales complètes l'onde réalise-t-elle entre l'émetteur et le fond du port ? ½n = 1100 /2 = 550 périodes spatiales. La précision du compteur étant d'une oscillation, déterminer l'incertitude de la mesure de la profondeur de l'eau dans le port. h = ½n c / f ; Dh/h = D n/ n =1/1100 ~ 10-3 ( 0,1 %). Une mesure en mer donne n = 110 000. Quelle est la profondeur de l'océan à cet endroit ? h = 0,5*110 000 *1,45 103 / 40000 =2,00 103 m. Si le nombre de période est 100 fois plus grand, la profondeur est 100 fois plus grande. L'amplitude de la pression P associée à l'onde ultrasonore diminue lors de sa progression et peut être modélisée par l'expression mathématique suivante : P= P0 exp(-µ L) P est l'amplitude de la pression lorsque l'onde a parcouru une distance L ; P0 = 10,0 Pa est l'amplitude de la pression au niveau de l'émetteur et µ =2,50 10-4 m-1 est le coefficient d'amortissement du milieu. Le récepteur est capable de détecter une onde dont l'amplitude de la pression est supérieure à Pmin = 1,0.10-3 Pa. Déterminer l'amplitude de l'onde reçue lors de la mesure précédente en admettant que le coefficient de restitution par le fond de l'océan est égal à 1. P = 10,0 exp(-2,50 10-4 *4000) =3,68 Pa. Quelle profondeur maximale le sonar peut-il en principe mesurer ? Commenter ce résultat. 1,0.10-3 = 10,0 exp(-2,50 10-4 L) ; ln 10-4 = -9,21 = -2,50 10-4 L ; L =3,68 104 m ; h = ½L =1,84 104 m = 18,4 km. Le sonar est capable de cartographier tous les fonds océaniques ( profondeur inférieure à 11 km).

retour -menu