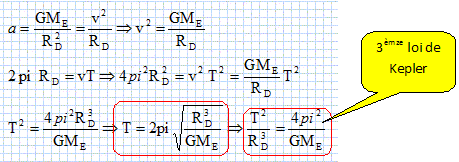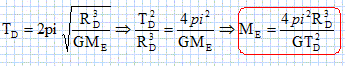|
Le cercle des planètes disparues ( bac S Liban 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
|
|||||||
|
Le 5 janvier 2005, une équipe d'astronomes a découvert sur des photographies prises le 21 octobre 2003 un nouveau corps gravitant autour du Soleil. Provisoirement nommé 2003 UB313, cet astre porte maintenant le nom d'Éris du nom de la déesse grecque de la discorde. La découverte d'Éris et d'autres astres similaires (2003 EL. 61, 2005 FY9...) a été le début de nombreuses discussions et controverses acharnées entre scientifiques sur la définition même du mot " planète ". Au cours d'une assemblée générale, le 24 août 2006 à Prague 2500 astronomes de l'Union Astronomique Internationale (UAI) ont décidé à main levée de déclasser Pluton comme planète pour lui donner le rang de " planète naine " en compagnie d'Éris et de Cérès (gros astéroïde situé entre Mars et Jupiter). Orbite d'Éris. Éris parcourt une orbite elliptique autour du Soleil avec une période de révolution TE valant environ 557 années terrestres. Données : Période de révolution terrestre : TT =1,00 an ; période de révolution de Pluton : TP = 248 ans. Énoncer précisément la troisième loi de Kepler, relative à la période de révolution d'une planète autour du Soleil, dans le cas d'une orbite elliptique. T2/a3 = 4pi2 / (GM )= constante. T : période de révolution ; a : demi-grand axe de l'ellipse ; M : masse de l'astre central, le soleil dans ce cas ; G : constante de gravitation. L'orbite d'Éris se situe-t-elle au-delà ou en-deçà de celle de Pluton ? Justifier sans calcul. a3 =T2/ constante. Le cube du demi-grand axe de l'ellipse est proportionnel au carré de la période de révolution. TE ~ 557 années terrestres et TP = 248 ans ; TE > TP : donc aE > aP et l'orbite d'Eris se situe au delà de celle de Pluton. Les astronomes ont découvert ensuite qu'Éris possède un satellite naturel qui a été baptisé Dysnomia (fille d'Éris et déesse de l'anarchie...). Six nuits d'observation depuis la Terre ont permis de reconstituer l'orbite de Dysnomia. On obtient la photographie ci-dessous.
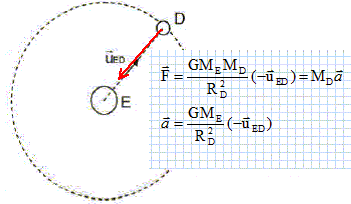
ME et MD sont les masses respectives d'Eris et de Dysnomia Masse de Pluton : MP = 1,31.1022 kg ; rayon de l'orbite circulaire de Dysnomia RD = 3,60.107 m Période de révolution de Dysnomia : TD = 15,0 jours ~ 1,30.106 s Constante de gravitation universelle : G = 6,67.10-11 m3.kg-1.s-2. Mouvement de Dysnomia. Le mouvement de Dysnomia autour d'Eris est supposé circulaire et uniforme. Définir le référentiel permettant d'étudier le mouvement de Dysnomia autour d'Éris. Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes. Le référentiel "Erisocentrique" a pour origine le centre d'Eris et des axes parallèles à ceux du référentiel héliocentrique. On étudie le mouvement deDysnomia dans le référentiel est "Erisocentrique". Par la suite, ce référentiel sera considéré comme galiléen. Établir l'expression du vecteur accélération du centre d'inertie de Dysnomia en fonction des paramètres de l'énoncé et d'un vecteur unitaire représenté sur le schéma ci-dessous. Dysnomia n'est soumis qu'à la seule force de gravitation due à Eris. Ecrire la seconde loi de Newton suivant l'axe défini sur la figure.
Préciser la direction et le sens de ce vecteur accélération. Le vecteur accélération est centripète, dirigé vers le centre d'Eris.
Montrer que la période de révolution TD de Dysnomia a pour expression TD = 2 pi [R3D / (GME)]½ . Retrouve-t-on la troisième loi de Kepler ? Justifier. Le mouvement étant circulaire uniforme, la circonférence 2 pi RD est décrite à la vitesse v en une période T.
|
|||||||
|
|
|||||||
|
|