Mesure de la hauteur d'un building à l'aide d'un baromètre. concours mines 06

sans calculatrice.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

Le fluide étudié ici est l’atmosphère terrestre. Le principe fondamental de la statique des fluides s’écrit ici :

dP/dz= -r g.

(si l’axe Oz est dirigé verticalement vers le haut, où P est la pression, r la masse volumique du fluide et g la norme du champ de pesanteur terrestre).

On assimile localement l’air à un gaz parfait isotherme à la température T₀.

Quelle est l’expression de la masse volumique r en fonction de la masse molaire de l’air M, de la pression P, de la constante des gaz parfaits R et de la température T₀ ?

Loi des gaz parfaits : P V = nRT₀ soit P = n/V RT₀

masse volumique : r = m/V ; n= m/M ( quantité de matière (mol) = masse (g) / masse molaire (g/mol) )

d'où : P= m/V RT₀/M ; P= r RT₀/M ; r = PM/(RT₀).

La masse molair de l'air est 29 g/mol. Justifier.

L'air contient : fraction molaire du dioxygène 0,2 ; fraction molaire du diazote : 0,8.

M(O₂) = 32 g/mol ; M(N₂) = 28 g/mol.

M(air) = 0,2*32+0,8*28 proche 29 g/mol.

Déduire, des questions précédentes, l’expression littérale de la pression en fonction de l’altitude z, de M, g, R, T₀ et P₀

(pression atmosphérique au niveau du sol), en admettant que g reste constant dans l’atmosphère.

dP/dz= -r g et r = PM/(RT₀).

d'où : dP/dz = -PMg/(RT₀) ; dP/ P = -Mg/(RT₀) dz ; d ln (P) = -Mg/(RT₀) dz

ln P = -Mg/(RT₀) z + Cte.

si z=0; P= P₀ d'où : ln (P/P₀) = -Mg/(RT₀) z.

P = P₀ exp(-Mg/(RT₀) z).

Justifier l’hypothèse ‘g constant’ (on donnera un ordre de grandeur de l’épaisseur de la couche atmosphérique).

g₀ = GM/R² ;g = GM/(R+z)² ; d'où g = g₀ [1+z/R]^-2.

L'épaisseur de l'atmosphère est voisine de z = 30 km et le rayon terrestre vaut R= 6400 km.

En conséquence z/R est proche de zéro et g proche de g₀ pour une altitude inférieure à 30 km.

Le baromètre indique une pression de P0 = 1 010 mbar au niveau du sol et P = 950 mbar en haut de la tour. En déduire que la hauteur H de celle-ci peut s’écrire sous la forme approchée : H = k(P0-P) / P0. où k est une constante dont on définira l’unité, la valeur approximative et la signification.

P = P₀ exp(-Mg/(RT₀) z).

P₀ étant proche de P, l'exponentielle est proche de 1 : -Mg/(RT₀) z est proche de zéro.

Effectuer un développement limité de l'exponentielle à l'ordre 1, au voisinage de zéro :

P=P₀ (1 -(Mg/(RT₀) z) ; P / P₀ =1 -(Mg/(RT₀) z ; 1-P / P₀ =(Mg/(RT₀) z

(P₀-P) / P₀ = (Mg/(RT₀) z ; z = RT₀ /(Mg)(P₀-P) / P₀ = k(P₀-P) / P₀.

k = RT₀ /(Mg).

(P₀-P) / P₀ : grandeur sans unité ; z : hauteur en mètre ; k s'exprime donc en mètre.

Donner l’ordre de grandeur de H.

Données numériques : g = 10 m.s^-2, R = 8,31 S.I et T₀ = 300 K.

M = 0,029 kg/mol ; k= 8,31*300/(0,029*10) proche de : 8600 m.

(P₀-P) / P₀= 60/1010 proche de 0,06 ; d'où z=H proche de : 8600*0,06 soit 520 m.

Utilisation indirecte du baromètre.

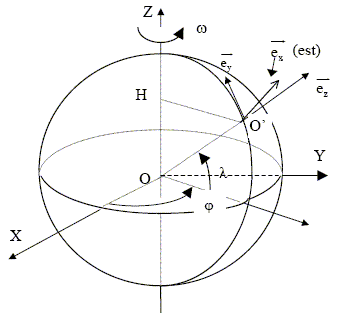
On se propose ici d’étudier la chute libre du baromètre depuis le sommet du building sans vitesse initiale et en l’absence de frottement.

Soit le référentiel géocentrique O, X, Y, Z. où O est le centre de la Terre. Les axes OX, OY et OZ sont dirigés vers des étoiles fixes.

Le référentiel géocentrique O, X, Y, Z est supposé galiléen.

Les grandeurs écrites en gras et en bleu sont des vecteurs.

Le référentiel terrestre de base (O’,e_x, e_y, e_z) est tel que : O’ est à la surface de la Terre, e_x est dirigé vers l’est (e_x rentre dans la feuille), e_y est dirigé vers le nord, e_z passe par le centre de la Terre.

L’angle l définit la latitude du point O’ (c’est l’angle entre e_z et le plan équatorial).

La Terre effectue un tour sur elle-même à la vitesse angulaire constante w = d.j/dt ˜ 7.10^-5 rad.s^-1.

j est l’angle entre OX et la projection de e_z dans le plan OXY.

Le référentiel terrestre n’est donc pas galiléen.

On lâche le baromètre de masse m depuis une altitude H, sans vitesse initiale.

Exprimer les composantes du vecteur rotation w dans la base (O’,e_x, e_y, e_z) en fonction de w et l.

w = 0 e_x+ wcosl e_y+ wsinl e_z.

Soient x, y, z, les composantes de M dans le référentiel terrestre.

Exprimer les composantes des trois forces appliquées à l’objet M.

poids : P = 0 e_x+ 0 e_y- mg e_z.

force d'inertie d'entraînement : F_e = 0 e_x-mw²(R+z) cosl sinl e_y+ mw²(R+z)cos²l e_z.

force de Coriolis : F_c = m (-2w z' cosl+2w y' sinl)e_x-2mw x' sinl e_y+2 mw x' cosl e_z.

En déduire les équations différentielles rigoureuses vérifiées par x, y, z et leurs dérivées par rapport au temps.

x"=-2w z' cosl+2w y' sinl (1)

y"= -w²(R+z) cosl sinl- 2w x' sinl (2)

z"= -g+ w²(R+z)cos²l+2 w x' cosl (3)

Dans le système d’équations différentielles précédent, quels termes peut-on négliger ? (On précisera par rapport à quoi on les néglige)

z et x sont très inférieurs au rayon terrestre R, donc R+z proche de R.

w²R = 49.10^-10 *6,4 10⁶ proche 0,03 ; donc w²R négligeable devant g.

y' << z' et on ne prend en compte que la composante de la force de Coriolis suivant e_x .

Simplifiez alors le système d’équations différentielles et le résoudre littéralement en fonction de H, w,l, g et R.

x"= -2w z' cosl (1)

y"= -w²R cosl sinl (2)

z"= -g (3)

z = -½gt²+Cte ( la constante est nulle car l'origine O' est à l'altitude H )

(2) donne : y = -½w²R cosl sinl t²

(1) donne : x"= 2w coslg t

x' = w coslgt² ; x=1/3w coslg t³

Au bout de combien de temps le baromètre touche-t-il le sol ?

On donne : H = 500 m, l= 30° (sin 30° = 0,5 et cos 30° ˜ 0,9), g ˜ 10 m.s^-2.

Au sol z = -H = -500 m ; 500 = 0,5*10 t² ; t² = 100 ; t = 10 s.

x₁ = 1/3 *7 10^-5*0,9*10*10³ = 0,7*0,3 = 0,021 m = 21 cm.

y₁ = -0,5*49 10^-10 *6,4 10⁶*0,5*0,9*100 = -0,5*0,49*6,4*0,5*0,9 =-0,70 m = - 70 cm.

Si on fait l’expérience, on constate que, selon la direction , le baromètre n’est absolument pas dévié par rapport à la direction d’un fil à plomb.

Pour quelle raison ?

Le fil a plomb prend en compte la force d'inertie d'entraînement.