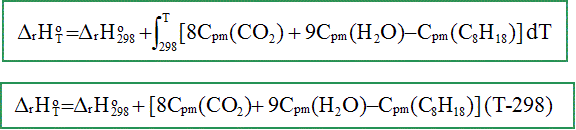Aurélie 13/12/07
 

Combustion isobare du mélange air essence ; thermochimie de la silice concours mines 06

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

Dans cette partie, on reprend l’étude du moteur à explosion et plus précisément celle de l’étape BC de combustion du mélange air-carburant

Le mélange gazeux est constitué de n = 4.10-2 mol d’air et de n’ = 2.10-4 mol d’essence et se trouve alors dans les conditions :

VB = 0,125 L ; TB = 673 K ; PB = 18,4 bar

Le gaz subit alors la transformation : B --> C : une étincelle provoque la combustion isobare, instantanée, de toute l’essence ; cette évolution est également adiabatique pour l’ensemble du système réactif.

Remarque : la combustion étant en réalité isochore et non isobare, on ne s’étonnera pas de trouver une température TC sensiblement différente de celle proposée dans le problème de physique.

Données : R=8,314 J K-1 mol-1. A 298 K :
Composé
C8H18(g)
CO2(g)
H2O(g)
DfH° ( kJ/mol)
580
-394
-242
Cp m ( J K-1 mol-1)
29
29
29
Les Cp,m , capacités thermiques molaires à pression constante, seront considérées indépendantes de la température.

Le carburant utilisé est de l’octane C8H18.

Ecrire et équilibrer la réaction de combustion d’une mole d’octane avec le dioxygène de l’air pour former CO2(g) et H2O(g).

C8H18(g) + 12,5O2(g) = 8 CO2(g) + 9 H2O(g)

Calculer l’enthalpie standard de cette réaction à 298K.

DrH° = 9 DfH° (H2O) + 8 DfH°(CO2)- DfH°(C8H18)

DrH°298 = 9*(-242)+8*(-394)-580 = -5,91 103 kJ /mol.

Exprimer puis calculer l’enthalpie standard de cette réaction à TB.

 
DrH°673 =  DrH°298 + 16*29.(673-298)

DrH°673 = -5,91 106 +1,74 105

DrH°673 = -5,736 106 J/mol = -5,736 MJ mol-1.
L’air est composé, en pourcentage molaire, de 20% de O2 et de 80% de N2 .

Justifier que l’énergie thermique dégagée par la combustion de l’octane sert à échauffer les gaz de combustion de TB à TC .

La transformation est adiabatique : pas d'échange d'énergie avec le milieu extérieur.

L'énergie dégagée par la combustion sert à élever la température des produits et du diazote.

Faire un bilan molaire des espèces présentes en début puis en fin de combustion.

Initial : n = 4.10-2 mol d’air et de n’ = 2.10-4 mol d’essence

n(O2)= 4.10-2*0,2 =8 10-3 mol ; n(N2)= 4.10-2*0,8 =3,2 10-2 mol.
avancement (mol)
C8H18(g)
+ 12,5 O2(g)
= 8 CO2(g)
+ 9 H2O(g)
initial
0
2.10-4
8 10-3
0
0
final
xfin
2.10-4 -xfin
8 10-3 -12,5xfin
8xfin
9xfin
2 10-4
0
5,5 10-3
1,6 10-3
1,8 10-3
si O2 est en défaut : 8 10-3 -12,5xfin =0 ; xfin = 8 10-3 /12,5 = 6,4 10-4 mol.

si C8H18 est en défaut : 2 10-4 -5xfin =0 ; xfin = 2 10-4 mol.

Retenir la plus petite valeur xfin = 2 10-4 mol.

Justifier la phrase : « Dans toute l’étude de ce modèle de moteur à explosion, on suppose constant le nombre total de moles gazeuses ».

Initial : n+n' = 4.10-2 + 2.10-4 = 4,02 10-2 mol.

Final : 5,5 10-3 +1,6 10-3 +1,8 10-3 +3,2 10-2 = 4,09 10-2 mol.

Le nombre total de mol est pratiquement le même.

 
En déduire la température TC en fin de combustion.

 Energie libérée par la combustion de l'essence : Q= n' |DrH°673 |= 2.10-4 *5,736 106 =1147 J.

Transformation isobare adiabatique : Q= ntotal Cp m DT = 4,0 10-2*29 DT =1,16 DT

DT= 1147/1,16 = 989 K ; TC = TB +989 =673+989 =1662 K.  
Thermochimie de la silice.

Les tables thermodynamiques donnent les enthalpies standard de formation suivantes (à 298K) :  
Si(s)
SiO2(s)
O2(g)
DfH° ( kJ/mol)
0
-911
0
 

Pourquoi les enthalpies de formation du silicium et du dioxygène sont nulles ?

Il s'agit de corps purs simples pris dans leur état standard à 298 K. Leur enthalpie de formation est nulle, par définition.

La liaison Si – O présente une énergie de liaison ESi-O= 796 kJ mol-1. L’énergie de la liaison O = O vaut EO=O= 498 kJ mol-1. On rappelle que l’énergie de liaison est l’énergie à fournir pour casser une mole de liaison, les constituants étant tous à l’état gazeux.

On donne l’enthalpie de sublimation du silicium : DsubH° (Si) =399 kJmol-1.

Etablir un cycle thermodynamique et donner alors l’expression littérale et la valeur numérique de l’enthalpie de sublimation de la silice.

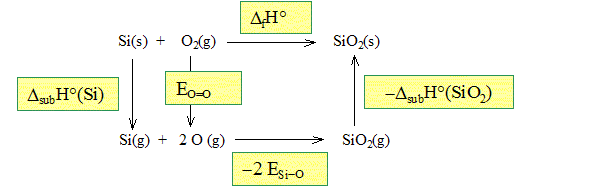
DfH°=DsubH° (Si) + EO=O -2ESi-O -DsubH° (SiO2).

DsubH° (SiO2)=DsubH° (Si) + EO=O -2ESi-O -DfH°.

DsubH° (SiO2)= 399 + 498-2*796-(-911)

DsubH° (SiO2)= 216 kJ/mol.


retour -menu