|
Etude de la réaction d’oxydation d’un mélange de fructose et de glucose par les ions molybdate concours Mines 05 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
Le fructose noté F ainsi que le glucose G réduisent le molybdène (VI) présent sous la forme d’ions molybdate MoO42- en molybdène (V) MoO2+ ou bleu de molybdène selon les réactions symbolisées : F+Mo(VI) --> Mo(V) +F' constante de vitesse kF. G+Mo(VI) --> Mo(V) +G' constante de vitesse kG. Ces deux réactions présentent la même loi cinétique, on note a et b les ordres partiels respectivement par rapport au sucre et au molybdène (VI). Donner la configuration électronique du molybdène (Mo : Z=42), indiquer sa position dans la classification périodique. 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s1 4d5 5è ligne ; 6è colonne Donner la représentation de Lewis des ions molybdate. Quelle est la géométrie que l’on peut prévoir pour ces ions ? MoO42- : deux charges négatives ; Mo : 6 électrons de valence ; O : 6 électrons de valence.
type AX4 donc structure tétraèdrique. On désire déterminer l’ordre de ces réactions ainsi que leur constante de vitesse. Pour cela on exploite le fait que les solutions aqueuses de bleu de molybdène sont colorées et présentent une bande d’absorption à 720 nm. On suit alors l’évolution du milieu réactionnel par spectrophotométrie à cette longueur d’onde. L’absorbance de la solution est alors proportionnelle à la concentration en Mo(V), c’est à dire en sucre ayant réagi.
-d[F]/dt =
kF[F]a[Mo(VI)]b. -d[G]/dt =
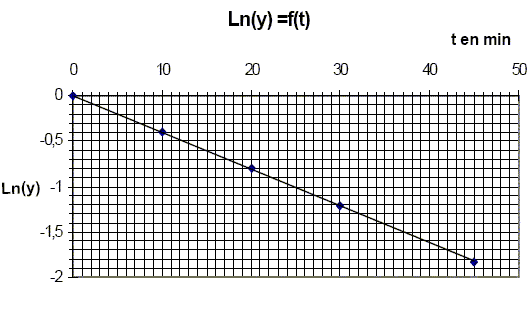
kG[G]a[Mo(VI)]b. calculer l'expression en fonction du temps du fructose ayant disparu à la date t. On notera kF' la constante apparente de vitesse. [Mo(VI)]b = constante ; kF' =kF[Mo(VI)]b ; -d[F]/dt = kF' [F] .d[F]/ [F] = - kF' dt, intégrer entre les instants t=0 et t. ln ( [F] /[F]0) = - kF' t ou [F] =[F]0exp(- kF' t). Dans la pratique nous mesurons [Mo(V)] en fonction du temps, donner son expression. F+Mo(VI) --> Mo(V) +F' [Mo(V)] =[F]0 -[F] = [F]0 (1-exp(- kF' t). De plus [Mo(V)]oo = [F]0 d'où : [Mo(V)] =[Mo(V)]oo(1-exp(- kF' t). On admettra que la réaction est finie au bout de 120 min et l'on posera [Mo(V)]oo = [Mo(V)]120. On fait une première série d’expériences en présence de fructose seulement. On introduit dans une fiole jaugée de 100 mL : 20 mL dune solution de fructose à 10-4 mol/L, 20 mL d’une solution de molybdate d’ammonium à 10-2 mol/L, 10 mL d’une solution d’acide sulfurique à 4,5 mol/L et l’on complète à 100 mL avec de l’eau distillée. On verse 5 mL de la solution obtenue dans 5 tubes à essais parfaitement propres et secs. On porte cette solution pratiquement instantanément à 100°C, puis aux dates de 10 min, 20 min, 45 min, 120 min, on plonge un tube dans un bain d’eau glacée, puis on mesure l’absorbance de la solution obtenue. On trace alors Ln(y)=f(t),où y= 1-[Mo(V)] /[Mo(V)]oo.
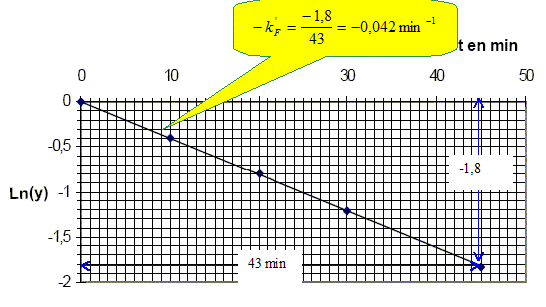
Quelle est l’influence de la température sur la vitesse d’une réaction ? La température est un facteur cinétique : la constante de vitesse suit la loi k = Cte exp(-EA/(RT) avec EA énergie d'activation. Pourquoi refroidit-on brutalement le milieu réactionnel avant d’effectuer la mesure ? On réalise une trempe, blocage cinétique. Que penser de l’hypothèse faite sur l’ordre partiel de la réaction par rapport au fructose ? [Mo(V)] =[Mo(V)]oo(1-exp(- kF' t) ; 1-[Mo(V)] / [Mo(V)]oo = exp(- kF' t) ; y =1-[Mo(V)] / [Mo(V)]oo ; y = exp(- kF' t) ; ln y = - kF' t La courbe correspondante est une droite passant par l'origine et de coefficient directeur - kF' : l'hypothèse est donc vérifiée. Calculer la constante apparente de vitesse kF’, préciser son unité.
On pose alors comme précédemment y =1-[Mo(V)] / [Mo(V)]oo , montrer alors que y varie linéairement en fonction de la fraction molaire initiale de fructose dans le mélange. F+Mo(VI) --> Mo(V) +F' constante de vitesse kF. G+Mo(VI) --> Mo(V) +G' constante de vitesse kG. [Mo(V)] =[F]0(1-exp(- kF' t) + [G]0(1-exp(- kG' t) [Mo(V)] = [F]0+[G]0-[F]0exp(- kF' t)- [G]0exp(- kG' t) [F]0+[G]0=[Mo(V)]oo ; [Mo(V)]-[Mo(V)]oo = -[F]0exp(- kF' t)- [G]0exp(- kG' t) y=([Mo(V)]oo-[Mo(V)])/ [Mo(V)]oo) = [F]0/ [Mo(V)]oo exp(- kF' t)+ [G]0/ [Mo(V)]ooexp(- kG' t) y= [F]0/ ([F]0+[G]0) exp(- kF' t)+ [G]0/ ([F]0+[G]0) exp(- kG' t) y =xF0exp(- kF' t)+xG0exp(- kG' t) or xG0 +xF0 =1 soit xG0 = 1-xF0 ; y= xF0exp(- kF' t)+exp(- kG' t)-xF0exp(- kG' t) y= xF0[exp(- kG' t)-exp(- kF' t] +exp(- kG' t). A une date t donnée, y est une fonction affine de xF0.
En déduire qu'il est possible de déterminer kF' et kG' en mesurant y à un instant donné t pour différentes valeurs du rapport xF0. y est une droite dont l'ordonnée l'origine est égale à : exp(- kG' t). De plus, si xF0 =1, alors y =exp(- kF' t). On obtient expérimentalement en prenant t = 45 min : kG' = 3,6.10-3 min-1. Que constate-t-on ? kF' = 4,2 10-2 min-1 , c'est à dire environ 10 fois plus grande que kG' Cela est mis à profit pour réaliser un dosage différentiel du fructose et glucose dans le sang.
|
|||||||
|
|
|||||||
|
|