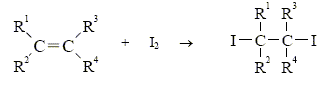Etude cinétique de l'addition du diiode sur un alcène concours Mines 04

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

Le le but de l’étude est de déterminer l’influence de la nature de l’alcène et du solvant sur l’ordre partiel de la réaction par rapport au diiode, sur la constante k de la réaction et sur le temps de demi-réaction t_1/2.

Le principe de la manipulation est le suivant :

- A la date t = 0, du diiode I₂ est mis à réagir sur l’un des alcènes étudiés dans un solvant donné.

- A des dates t successives, on effectue des prélèvements du milieu réactionnel que l’on dose par une solution aqueuse de thiosulfate de sodium Na₂S₂O₃ afin de déterminer la quantité de diiode n’ayant pas encore réagi.

- L’allure de différentes courbes faisant intervenir des fonctions de [I₂] et t permet de déterminer l’ordre de la réaction, sa constante de vitesse k et le temps de demi-réaction t_1/2 pour un couple alcène-solvant donné.

Le protocole opératoire utilisé pour chaque couple solvant-alcène est le suivant :

(1) Mise en route de la réaction d’addition

A la date t = 0, sont mis en présence dans un erlenmeyer de 250 mL, 50 mL d’une solution à 0,6 mol.L^-1 d’alcène dans le solvant d’étude et 50 mL de solution à 0,04 mol.L^-1 de diiode I₂ dans le solvant d’étude. On laisse la réaction se faire, sous agitation, à la température constante de 25 °C.

(2) Dosages réalisés à différentes dates t :

A 25 mL d’une solution aqueuse de iodure de potassium K⁺,I^- à 0,12 mol.L^-1, on ajoute v₀ = 5 mL de solution prélevée depuis le milieu réactionnel. La date t est relevée au moment où la pipette de 5 mL contenant le prélèvement est à moitié vidée. La solution ainsi préparée est immédiatement titrée par une solution aqueuse de thiosulfate de sodium Na₂S₂O₃ à c = 0,01 mol.L^-1. A l’équivalence du dosage la coloration jaune de la solution titrée disparaît. Le volume correspondant à l’équivalence du dosage est relevé.

Etude théorique de la loi de vitesse suivant que la réaction est d’ordre partiel 1, 2 ou 3 par rapport au diiode I₂.

Donner la définition de la vitesse volumique v de réaction en utilisant les concentrations de chacun des réactifs.

v = - d[I₂]/dt = -d[alcène]/dt.

Donner l’expression de la vitesse de réaction, sachant que la réaction admet un ordre partiel n par rapport au diiode I₂ et un ordre partiel p par rapport à l’alcène.

Que vaut l’ordre global ?

v = k[I₂]ⁿ[alcène]^p : odre global : n+p.

Montrer que, dans le milieu réactionnel, l’alcène est introduit en large excès par rapport au diiode.

[alcène]₀ = 0,6 mol/L ; [I₂]₀ = 0,04 mol/L soit 15 fois plus petit que [alcène]₀.

Montrer que l’expression de la vitesse de réaction peut alors se mettre sous une forme simplifiée, faisant apparaître une constante de vitesse apparente, que l’on notera k_app.

[alcène] proche [alcène]₀ = 0,6 mol/L ; v = k[alcène]₀^p [I₂]ⁿ

v = k_app [I₂]ⁿ avec k_app = k[alcène]₀^p.

De quelle technique de détermination d’un ordre s’agit-il ici ?

Dégénerescence de l'ordre.

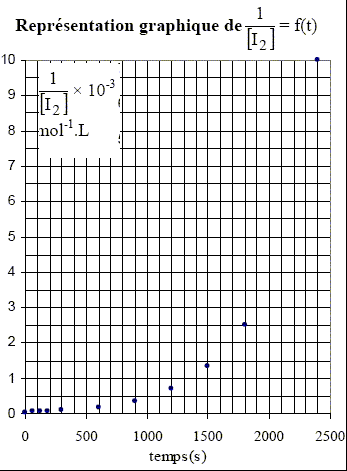
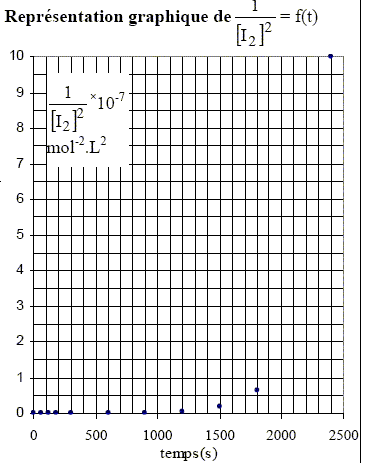
Dans l’hypothèse d’une réaction d’ordre partiel n = 1 par rapport au diiode, donner l’expression donnant l’évolution de la concentration en diiode au cours du temps t, en fonction de [I2]0, concentration initiale en diiode dans le milieu réactionnel, kapp et t. d[I2]/dt = -kapp [I2] ;  dln[I2]= -kapp dt ln([I2]/[I2]0) = -kappt.

Quelle fonction de la variable [I₂] faut-il représenter en fonction de t pour obtenir comme représentation graphique une droite si la réaction est bien d’ordre 1 par rapport à I₂ ?

ln([I₂]/[I₂]₀) = f(t) ; droite de coefficient directeur -k_app.

donner l’expression donnant l’évolution de la concentration en diiode au cours du temps t,

en fonction de [I₂]₀, concentration initiale en diiode dans le milieu réactionnel, k_app et t.

d[I₂]/dt = -k_app [I₂]² ;  d(-1/[I₂])= -k_app dt

1/[I₂]₀-1/[I₂] = -k_app t ; 1/[I₂]-1/[I₂]₀ = k_app t.

Quelle fonction de la variable [I₂] faut-il représenter en fonction de t pour obtenir comme représentation graphique une droite si la réaction est bien d’ordre 2 par rapport à I₂ ?

1/[I₂] = f(t) ; droite de coefficient directeur k_app.

Quelle fonction de la variable [I2] faut-il représenter en fonction de t pour obtenir comme représentation graphique une droite si la réaction est bien d’ordre 3 par rapport à I2 ?

Dans l’hypothèse d’une réaction d’ordre partiel n = 32 par rapport au diiode, donner l’expression donnant l’évolution de la concentration en diiode au cours du temps t, en fonction de [I2]0, concentration initiale en diiode dans le milieu réactionnel, kapp et t. d[I2]/dt = -kapp [I2]3 ;  -½ d(1/[I2]2)= -kapp dt 1/[I2]20-1/[I2]2 = -2kapp t ; 1/[I2]2-1/[I2]20 =2kapp t. Quelle fonction de la variable [I2] faut-il représenter en fonction de t pour obtenir comme représentation graphique une droite si la réaction est bien d’ordre 3 par rapport à I2 ? 1/[I2]2 = f(t) ; droite de coefficient directeur 2kapp.

Dosage du diiode restant par le thiosulfate de sodium.

Les solvants utilisés ici sont non miscibles à l’eau.

La solubilité du diiode I₂ dans l’eau est assez faible, elle est bien plus importante dans les solvants organiques utilisés ici.

Comment expliquer la faible solubilité du diiode dans l’eau ?

Le diiode, molécule apolaire est peu solule dans un solvant polaire comme l'eau.

Quelle est la nature précise des interactions existant entre les molécules d’eau et une molécule de diiode dissoute, entre molécules d’eau, entre molécules de diiode ?

Interactions de type Van der Waals entre molécules de diiode.

Interactions de type Van der Waal et diaisons hydrogène ( plus énergétiques) entre molécules d'eau.

Les molécules de diiode entourent d'autres molécules de diiode ; des molécules d'eau entouent d'autres molécules d'eau.

Dans quelle phase se trouvent la majorité des molécules de diiode lorsqu’on est en présence d’un mélange non miscible solvant organique-eau ?

Les molécules de diiode apolaires ont une grande affinité pour un solvant organique peu polaire ; le diiode est donc majoritairement dans la phase organique.

On accroît fortement la solubilité de I₂ dans l’eau en ajoutant de l’iodure de potassium KI en raison de l’existence d’un équilibre de complexation :

I₂ + I^- = I₃^- ; K_f = 10^2,9.

Déduire de ces informations, l’intérêt d’ajouter 25 mL d’une solution d’iodure de potassium au prélèvement avant de réaliser le titrage par une solution aqueuse de thiosulfate de sodium.  

Toutes les molécules de diiode passent dans la phase aqueuse sous forme d'ion I₃^- ; cet ion est ainsi au contact de l'ion thiosulfate, l'autre réactif, dans la phase aqueuse

La date t, à laquelle on dose la concentration en diiode restant est-elle précise ? Pourquoi faut-il réaliser le titrage le plus rapidement possible ?

Cette date est imprécise : le dosage du diiode dure quelques minutes.

Montrer que l’ajout de 25 mL d’une solution d’iodure de potassium à 5 mL de milieu réactionnel permet, en plus de l’intérêt mentionné à la question précédente, d’améliorer la précision sur la date t.

La concentration des réactifs est un facteur cinétique : en diluant la solution ( ajout de 25 mL de KI), les concentrations, et en conséquence la vitesse, diminuent.

Que peut-on proposer d’autre pour améliorer la précision sur cette date t ?

Une trempe ( refroidissement brutal) réalise un blocage cinétique.

Lors du dosage du diiode restant par le thiosulfate de sodium Na₂S₂O₃, les couples mis en jeu sont I₃^-/I^- et S₄O₆^2-/S₂O₃^2-.

Déterminer le degré d’oxydation du soufre S dans l’ion thiosulfate S₂O₃^2-.

2 n.o(S) +3 n.o(O)=-2 ; 2 n.o(S)+3*(-2) = -2 ; 2 n.o(S) = -4 ; n.o(S) = +II.

L'un des atome de soufre est au degré d'oxydation -II, l'autre au degré d'oxydation +VI.

Ecrire l’équation bilan de la réaction de dosage.

I₃^- + 2e^- =3I^- réduction

2S₂O₃^2- = S₄O₆^2-+ 2e^- oxydation

2S₂O₃^2- +I₃^- = S₄O₆^2- + 3I^-

Etablir l’expression du potentiel d’oxydoréduction standard du couple I₃^-/I^- à 25°C

en fonction du potentiel d’oxydoréduction standard du couple I₂/I^- et de la constante de formation K_f de l’ion I₃^-.

I₂ + 2e^- =2I^- ; E₁ = E°(I₂/I^-) +0,03 log ([I₂]/[I^- ]².(1)

I₃^- + 2e^- =3I^- ; E₂ = E°(I₃^-/I^-) +0,03 log ([I₃^-]/[I^- ]³.

K_f = [I₃^-]/([I^- ][I₂]) ; [I₂] = [I₃^-]/([I^- ]K_f ) ; repport dans (1) :

E₁ = E°(I₂/I^-) +0,03 log ([I₃^-]/([I^- ]³K_f ).

E₁ = E°(I₂/I^-) -0,03 logK_f+ 0,03 log ([I₃^-]/([I^- ]³.

En déduire la valeur numérique du potentiel d’oxydoréduction standard du couple I₃^-/I^- à 25°C.

On identifie E°(I₂/I^-) -0,03 logK_f à E°(I₃^-/I^-).

E°(I₃^-/I^-) = 0,62 -0,03 *2,9 = 0,53 V.

Etablir l’expression de la constante de la réaction de dosage K° en fonction des potentiels d’oxydoréduction standard adéquats.

I₃^- + 2e^- =3I^- ; E₂ = E°(I₃^-/I^-) +0,03 log ([I₃^-]/[I^- ]³).

2S₂O₃^2- = S₄O₆^2-+ 2e^- ; E₃ = E°(S₄O₆^2-/S₂O₃^2-) +0,03 log ([S₄O₆^2-]/[S₂O₃^2- ]²).

A l'équilibe E₂=E₃ :

E°(I₃^-/I^-)-E°(I₃^-/I^-) =0,03 log ([S₄O₆^2-][I^- ]³/([S₂O₃^2- ]²[I₃^-])

2S₂O₃^2- +I₃^- = S₄O₆^2- + 3I^- K°=[S₄O₆^2-][I^- ]³/([S₂O₃^2- ]²[I₃^-])

E°(I₃^-/I^-)-E°(I₃^-/I^-) =0,03 log K

En déduire l’ordre de grandeur de sa valeur numérique. Cette réaction est-elle quantitative ? Commenter.

log K = (0,533-0,09)/0,03 = 14,8 ; K = 5,8 10¹⁴.

K est très grand : la réaction est quantitative ; si de plus, elle est rapide, elle peut servir de support d'un dosage.

Etablir la relation existant entre la concentration en diiode restant dans le milieu réactionnel à l’instant t et le volume v_eq de solution de thiosulfate de sodium versé à l’équivalence.

A l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoechiométriques.

n(S₂O₃^2-) = 2 n(I₃^-) ; n(I₃^-) = ½ [S₂O₃^2-] V_éq ; [I₃^-] = [I₂]= ½ [S₂O₃^2-] V_éq /v₀.

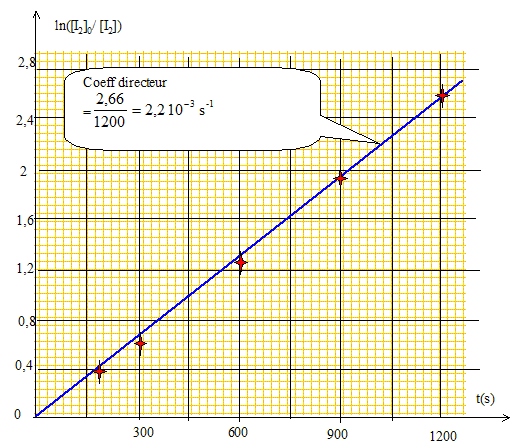
Le tableau (ci-dessous) indique les volumes équivalents relevés à différentes dates t pour la réaction d’addition de diiode sur le cyclohexène en solution dans le 1,2-dichloroéthane.

t(s)	0	60	120	180	300	600	900	1200	1500	1800	2400
véq(mL)	20	17,5	15,3	13,5	10,3	5,35	2,8	1,4	0,75	0,4	0,1

Peut-on déterminer, de manière certaine, l’ordre partiel par rapport au diiode de la réaction d’addition de diiode sur le cyclohexène en solution dans le 1,2-dichloroéthane à l’aide des courbes ci-dessus ?

Les courbes ci-dessus ne sont pas des droites, ce qui exclut les ordres 2 et 3.

Pour confirmer l'ordre 1, il faut tracer la courbe d'équation ln([I₂]₀/[I₂]) =f(t). Cette courbe doit être une droite.

[I₂]= ½ [S₂O₃^2-] V_éq /v₀ = 0,5*0,01/5 .V_éq = 10^-3 V_éq.

t(s)	0	60	120	180	300	600	900	1200	1500	1800	2400
véq(mL)	20	17,5	15,3	13,5	10,3	5,35	2,8	1,4	0,75	0,4	0,1
[I2]	[I2]0 =0,02	0,0175	0,0153	0,0135	0,0103	0,00535	0,0028	0,0014	0,00075	0,0004	10-4
[I2]0/[I2]	1	1,14	1,30	1,48	1,94	3,73	7,14	14,3	26,6	50	200
ln([I2]0/[I2])	0	0,133	0,27	0,39	0,66	1,32	1,96	2,66	3,3	3,9	5,3

Rappeler la définition du temps de demi-réaction t½. Déterminer l’ordre de grandeur de sa valeur numérique pour la réaction d’addition de diiode sur le cyclohexène en solution dans le 1,2-dichloroéthane à 25 °C.

Pour une réaction totale, le temps de demi-réaction est la durée au bout de laquelle la concentration initiale du diiode est divisée par deux.

ln([I₂]₀/[I₂]) = k_appt ; ln2 = k_appt_½ ; t_½ =ln2 / k_app=0,69/2,2 10^-3 = 314 s.