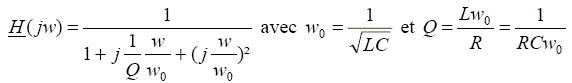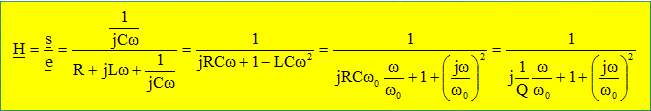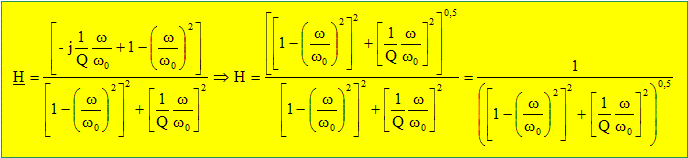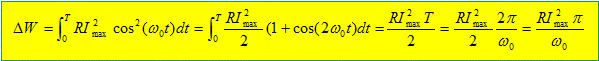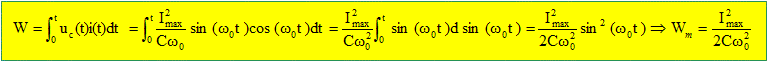|
facteur de qualité : étude d'un filtre passif, diagramme de Bode concours Mines 04 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
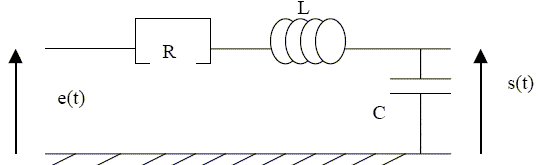
Il est composé de trois dipôles en série : une résistance R, une inductance parfaite de coefficient d’induction L, et d’un condensateur de capacité C.
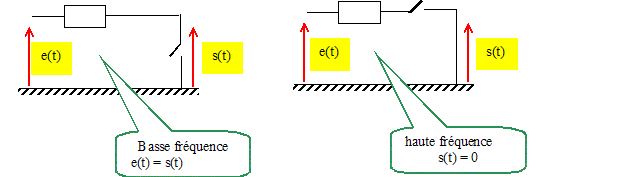
Il est soumis à une tension d'entrée sinusoidale e(t)=Em cos(wt+j). On note s(t) la tension de sortie. En notation complexe, on notera, pour e(t) par exemple, e= Em e(jwt) = Eejj e(jwt), Em : amplitude complexe. A l'aide de deux schémas équivalents du circuit, l'un en hautes frequences, l'autre en basses fréquences, donner la nature de ce filtre.
Le filtre coupe les hautes fréquences, mais laisse passer les basses fréquences : filtre passe bas. Etablir la fonction de transfert de ce filtre sous la forme :
Donner l’ordre de ce filtre.
Le dénominateur compte un terme en w2 : donc filtre d'ordre 2.
e =
1/(Qw0)
jw
+1/w02
(jw)2+1]s. à
jw
correspond ds/dt ; à (jw)2
correspond
d2s/dt2. d'où :
e(t)
=1/w02d2s/dt2
+1/(Qw0)
ds/dt + s(t) Pour quelle raison
peut-on affirmer la convergence du régime
transitoire ? 1/w02,
1/(Qw0),
1
sont de même
signe.
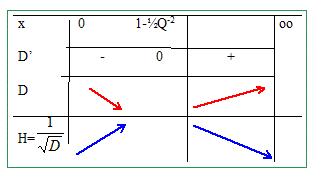
Montrer que H passe par un maximum pour Q >2-½.
résonance. Déterminer wr, la pulsation correspondant à ce phénomène, en fonction de w0 et Q. wr2/w20 = 1-½Q-2 ; wr = w 0[1-½Q-2]½.
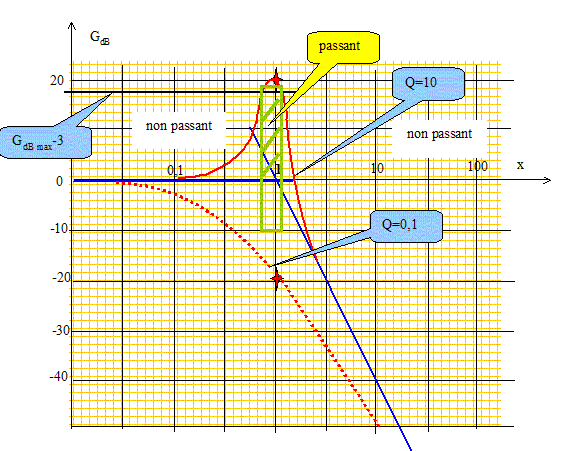
On appelle gain, la fonction , telle que GdB= 20 log H . Donner les équations des asymptotes de GdB aux basses fréquences et aux hautes fréquences. GdB= -10 log [(1-x2)2+Q-2x2 ] si x tend vers 0, alors GdB est équivalent à 0. L'axe des abscisses est asymptote horizontale. si x tend vers l'infini, alors GdB est équivalent à -40 log x. ( droite de pente -40 dB par décade). Cette droite asymptote coupe l'axe des abscisses en x=1. Exprimer GdB(w=w0). x=1 ; GdB(1) = -10 log Q-2 = 20 log Q. Tracer l’allure du diagramme de Bode en gain pour Q=10 et Q=0,1.
On définit les pulsations de coupures wc d’un filtre par la relation : H <Hmax / 2½. Justifier que la bande passante est alors définie à -3dB. gain pour la pulsation wc : GdB = 20 log ( Hmax* 2-½) =20 log Hmax -10 log 2 = 20 log Hmax -3 = GdB max-3.
Interprétation énergétique du facteur de qualité Q. On suppose Q >>1. Montrer que si w=w0, alors i(t) = Imax cos(w0t). Les fréquences de coupures sont proches de w0 ( résonance très aigue). Les effets capacitifs compensent les effets inductifs. L'impédance du dipôle est minimale, égale à R. L'intensité et la tension aux bornes du dipôle sont en phase. Déterminer alors uc(t), la tension aux bornes du condensateur en fonction de C, Imax et w0. La tension aux bornes du condensateur est retard de ½p sur l'intensité. Udipôle = R Imax ; Uc = Imax / (Cw0) = Udipôle / (RCw0) = Q.Udipôle. uc(t) = Imax / (Cw0) cos (w0t-½p ) = Imax / (Cw0) sin (w0t ) On note, DW l'énergie dissipée par effet Joule dans la résistance sur une période. Montrer que DW = p /w0RI2max.
On note Wm, l’énergie maximale reçue par le condensateur. Montrer que Wm =I2max/ (2Cw02).
En déduire que : Q = 2p Wm/DW. Wm/DW = 1/ (2pRCw0) ; or Q = 1/ (RCw0) d'où : Wm/DW = Q /(2p). Q = 2p Wm/DW.
|
|||||||
|
|
|||||||
|
|