|
Modélisation d'un oscillateur à quartz concours Mines 04 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
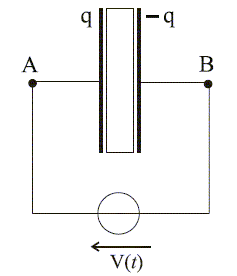
Modèles mécanique et électrique du résonateur à quartz. Un cristal de quartz est taillé sous forme de pastille cylindrique mince. La base circulaire présente un diamètre d=1 cm et l’épaisseur de la pastille est e=0,2 mm. Des électrodes métalliques (en or généralement) sont déposées sur chacune des faces circulaires du quartz (on suppose que ces faces sont totalement métallisées). On parle d’électrodes de connexion. On a ainsi réalisé un condensateur plan.
D’un point de vue mécanique, lorsque l’on soumet le disque piézo-électrique à une tension sinusoïdale V(t) = V·cos(w t) , il va être, dans le cadre d’une approximation linéaire, le siège d’une vibration mécanique sinusoïdale sous l’effet d’une force extérieure proportionnelle à cette tension. Modélisation proposée : un élément de masse m du corps piézo-électrique, placé à une distance x de son point de repos, est soumis aux forces suivantes, toutes orientées selon un axe (Ox) que l’on ne précise pas ici : • une force de rappel type élastique -kx (k>0)qui a pour origine la rigidité du matériau, • des frottements supposés proportionnels à la vitesse et de la forme -h dx/dt (h>0), • une force due à l’effet piézo-électrique bV(t) (b>0), • le poids est négligé.
En appliquant le principe fondamental de la dynamique au petit élément de masse m dans le référentiel du laboratoire supposé galiléen, établir l’équation différentielle vérifiée par x(t) en supposant que le mouvement se fasse selon l’axe (Ox). md2x/dt2 = -kx -hdx/dt +bV(t) d2x/dt2 + h/m dx/t + k/m x = b/m V(t). D'un point de vue électrique, la charge totale q apparaissant sur les électrodes planes a deux origines : . les deux faces planes du disque forment un condensateur de capacite CP, d'où une charge q1(t), . l'effet piezo-electrique provoque l'apparition d'une charge q2 proportionnelle à x : q2 =g x(t). On montre que la capacité d�'un condensateur plan vaut C=e0erS/ e où S est la surface d'une électrode, e l'épaisseur du condensateur, e0 la permittivite du vide (sa valeur est 8,85 10-12 Fm-1) et er une constante valant pour le quartz 2,3. - Estimer alors la capacité CP appelée capacité de connexion. S= pd2/4 =3,14 10-4 /4 =7,85 10-5 m2 ; e = 0,2 mm = 2 10-4 m ; CP=e0erS/ e =8,85 10-12 *2,3*7,85 10-5 / (2 10-4)=8,0 10-12 F. - Quelle est la relation entre la charge q1, la capacité CP et la tension V(t) ? q1=CPV(t). d2x/dt2 + h/m dx/t + k/m x
= b/m
V(t). q2 =g x(t)
; d2q2/dt2
=gd2x/dt2
; dq2/dt=gdx/dt
; d2q2/dt2
+h/mdq2/dt +k/m q2 =
g
b/m
V(t). m/
(g
b)
d2q2/dt2 +h/
(g
b)
dq2/dt +k/
(g
b)
q2 =
V(t).
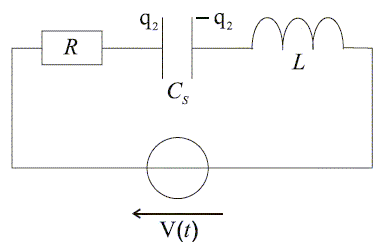
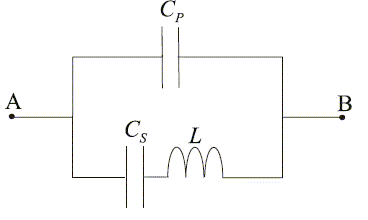
Montrer que la charge q2(t) est équivalente à la charge d'un condensateur de capacité CS dans le circuit série R, L, CS dont la tension aux bornes est V(t). On donnera alors les expressions de R, L et CS en fonction de m, h, g , b et k. additivité des tensions : V(t) = R i + q2/CS + Ldi/dt avec i = dq2/dt ; di/dt = d2q2/dt2. d'où : V(t) = Rdq2/dt + q2/CS + Ld2q2/dt2. On identifie : L à m/ (g b) ; R à h/ (g b) ; CS à g b/k . Etude de l’impédance équivalente du quartz : Dans cette partie, on néglige la résistance R du quartz. Le schéma électrique simplifié est alors donné ci-dessous. Pour les applications numériques, on prendra L = 500 mH, CS = 0,08 pF et CP = 8 pF.
Calculer alors l'impédance complexe du quartz, vue entre les bornes A et B. impédance complexe de chaque branche : 1/(jCPw) ; jLw + 1/(jCSw) Les admittances complexes correspondantes s'ajoutent.
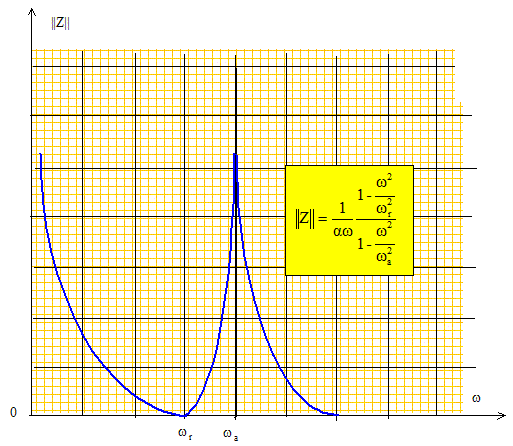
Montrer aussi que w2a >w2r. w2a /w2r =(CP+CS) /(CP) =1+CS/CP= 1+0,08/8 = 1,01.
wa =[ (8 10-12 + 8 10-14) / (0,5*8 10-12 * 8 10-14)]½ =5,02494 106 rad/s ; fa = wa /(2p) =7,99744 105 Hz. wr =[ 1 / (0,5*8 10-14)]½=5,0 106 rad/s ; fr = wr /(2p) =7,95775 105 Hz. Etudier le comportement inductif ou capacitif du quartz en fonction de la fréquence. On rappelle qu’un dipôle a un comportement inductif (respectivement capacitif) si la partie imaginaire de son impédance est positive (respectivement négative). Si w est compris entre wr et wa, la partie imaginaire de l'impédance est positive : le dipôle est inductif. En dehors de l'intervalle [wa ; wr ] le dipôle est capacitif. Tracer l’allure de ||ZAB||, module de l’impédance complexe du quartz, en fonction de la fréquence.
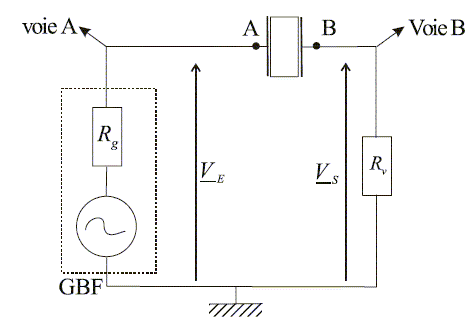
Etude expérimentale de la résonance d’un quartz : On veut tracer expérimentalement la courbe donnant l’impédance du quartz en fonction de la fréquence d’excitation. On dispose d’un générateur basses fréquences pouvant délivrer une tension sinusoïdale d’amplitude réglable. Le GBF possède une résistance interne Rg. On dispose d’une résistance Rv variable, d’un quartz et d’un oscilloscope. Dans cette question, on néglige toujours la résistance du quartz On réalise alors le montage suivant :
Calculer le rapport de la tension de sortie Vs à celle d'entrée VE : H =Vs /VE en fonction de Rv et de ZAB. H = Rv / (Rv+ZAB) = Rv [ (Rv+ZAB)] / (R2v+Z2AB) On choisit, pour chaque fréquence, la résistance Rv de telle facon que ||H||=0,5. Que vaut alors le module de l'impédance du quartz en fonction de Rv ? ||H||=Rv / (R2v+Z2AB)½ =0,5 0,25 (R2v+Z2AB) = R2v ; ||ZAB|| =3½Rv. Autour du pic de résonance d'intensité situé vers 796 kHz, on mesure une bande passante de 50 Hz. Quelle est la valeur numérique du facteur de qualité Q du quartz défini comme le rapport de la largeur de la bande passante à la fréquence de résonance ? Commenter cette valeur. Q = 7,96 105 /50= 1,6 104, valeur très élevée : la résonance est très aigue. En supposant que le facteur de qualité soit donné par la relation Q= Lw0/R (w0 étant la pulsation de résonance), estimer la valeur de la résistance R du quartz. w0 =2pf0 =6,28*7,96 105 =5,0 106 rad/s : L=0,5 H ; Q= 1,6 104. R = Lw0 /Q = 0,5*5,0 106 / 1,6 104 = 156 W.
Principe d’une montre à quartz : Une horloge est composée d’un oscillateur plus ou moins stable dans le temps et d’un système de comptage des oscillations. Le quartz utilisé présente une fréquence de résonance de 32768 Hz. Cela signifie que 32768 fois par seconde une impulsion électrique est émise par le circuit oscillant. Un dispositif électrique doit compter les impulsions. Ces compteurs fonctionnent dans la technologie binaire (suite de 0 et de 1). Une impulsion électrique correspond à la valeur 1. La valeur 0 correspond à aucun signal électrique. Compteur modulo 2 : Un tel compteur délivre une impulsion de sortie dès qu’il a compté 2 impulsions à son entrée. Si en entrée d’un tel compteur on envoie le signal à 32768 Hz délivré par le circuit à quartz, quelle est la fréquence du signal de sortie du compteur modulo 2 ? 32768 / 2 = 16384 Hz. Succession de compteurs modulo 2 : Ecrire le nombre 32768 sous la forme 2k où k est un entier naturel. 32768 = 215. Combien de compteurs modulo 2 faut-il alors mettre en cascade pour commander le chiffre des secondes ? 15 compteurs. |
|||||||
|
|
|||||||
|
|