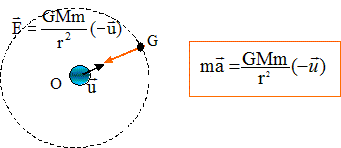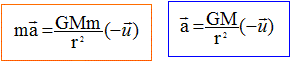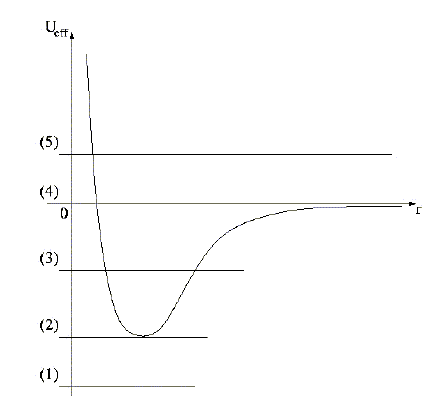|
Etude du mouvement de quelques satellites concours Mines 03 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
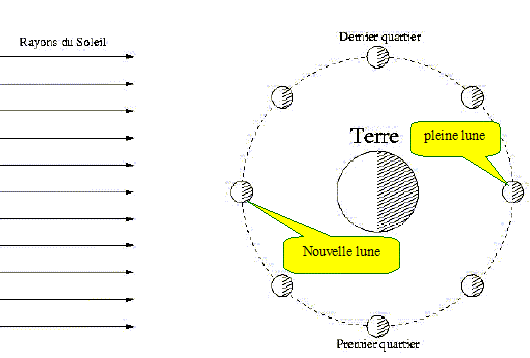
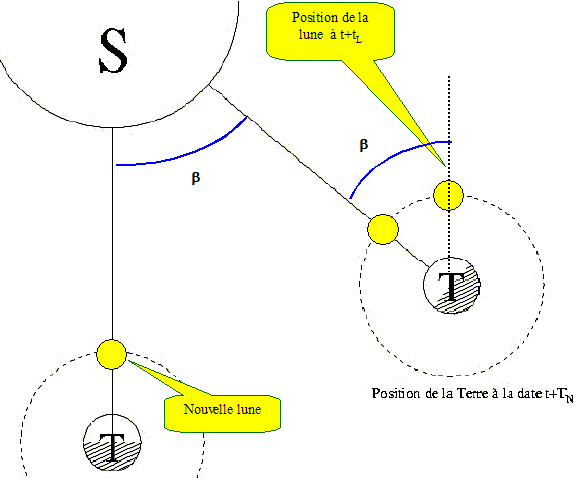
Cette partie se propose d’étudier quelques caractéristiques du mouvement des satellites terrestres. Dans cette partie, on désignera par MT et RT respectivement la masse et le rayon de la Terre. On donne RT = 6370 km, MT = 5,98.1024 kg. On rappelle que la constante de gravitation universelle a pour valeur G = 6,67.10-11 N.m2.kg-2. Mouvement de la Lune autour de la Terre. Le centre L de la Lune décrit, de manière uniforme, autour de la Terre, une orbite circulaire de centre T telle qu’en un jour le segment [TL] balaie un angle de 0,230 radian. Déterminer, en jours, la période TL de ce mouvement circulaire de la Lune autour de la Terre. TL correspond à 2p radians ; un jour corespond à 0,230 rad. d'où TL =2p /0,230 = 27,3 jours. Sachant que le rayon RTL de l’orbite circulaire décrite par la Lune est de 3,84.105 km, en déduire la valeur de la masse de la Terre 3è loi de Kepler : T2L/ R3TL = 4p2/(GMT). MT=4p2R3TL/(GT2L) avec RTL=3,84 108 m ; R3TL= 5,66 1025 ; TL =27,3*24*3600 =2,36 106 s ; T2L=5,57 1012. MT=4*3,142* 5,66 1025/(6,67.10-11 *5,57 1012) ; MT= 6,0 1024 kg. On sait que la Lune, dans son mouvement autour de la Terre, nous présente toujours la même face. En déduire les caractéristiques du mouvement propre de la Lune. La lune tourne sur elle même : elle effectue un tour en 27,3 jours. Le schéma suivant représente les différentes phases de la Lune. On dit que la Lune est nouvelle lorsque la face qu’elle présente à la Terre n’est pas éclairée. Identifier la nouvelle Lune sur ce schéma, et préciser comment elle est alors vue depuis la Terre. Sur le schéma (II) de la feuille annexe, dessiner les positions de la Lune lors des nouvelles lunes successives à t et t + TN. Dessiner aussi la position de la lune à la date t + TL.
En 27,3 jours, la terre décrit autour du soleil un angle b= 2p *27,3/365 =0,47 rad. La lune se retrouve à la position " nouvelle lune" lorsqu'elle a parcouru sur son orite un angle de 2p+0,47 = 6,75 rad. Ce qui correspond à : 6,75/0,23 = 29,4 jours.
En l’absence de précision explicite, on négligera tout frottement dû à l’atmosphère sur le satellite. On s’intéresse à un satellite artificiel, de masse m, en orbite circulaire de rayon R autour de la Terre. Montrer que le mouvement du satellite autour de la Terre est uniforme, et exprimer littéralement la vitesse v0. Schéma représentant la terre, le satellite sur sa trajectoire et la force exercée par la terre sur le satellite. On note r = R +h.
Référentiel d'étude du mouvement du satellite : géocentrique. L'origine du repère est le centre de la terre. La force de gravitation est centripète, perpendiculaire à la vitesse : la puissance de cette force est donc nulle. En conséquence, cette force ne modifie pas la valeur de la vitesse : le mouvement est uniforme. Expression du vecteur accélération a du point G.
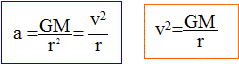
Caractéristiques du vecteur accélération d'un point matériel ayant un mouvement circulaire uniforme : Ce vecteur est appliqué au point G ; il est dirigé de G vers O : on dit que l'accélération est centripète. La valeur de l'accélération s'exprime par : a = v2/r. v : vitesse en m/s et r (m) rayon de l'orbite circulaire. Vitesse du satellite :
remarquons que GM = g0R2T. Le satellite SPOT (Satellite sPécialisé dans l’Observation de la Terre) est en orbite circulaire à l’altitude h = 832 km au-dessus de la Terre. Calculer numériquement la vitesse v0 de SPOT sur son orbite. r = 6,37 106 + 8,32 105 =7,53 106 m ; v=6,37 106.[9,81/7,02 106 ]½ =7,5 103 m/s.
La vitesse de libération vl d’un satellite est la plus petite vitesse qu’il faut lui communiquer à la surface de la Terre pour qu’il aille à l’infini (en « se libérant » de l’attraction terrestre). Exprimer vl en fonction de G, MT et RT et calculer sa valeur. Energie mécanique du satellite à la surface de la terre : EM= -GMTm/RT + ½mv2l. Energie mécanique du stellite à l'infini : EM=0. Conservation de l'énergie mécanique : -GMTm/RT + ½mv2l=0 v2l= 2GMT/RT ; vl= [2GMT/RT]½. vl =[2*6,67.10-11*5,98.1024/6,37 106]½ ; vl =11,2 103 m/s. Dans le cas d’une orbite circulaire du satellite autour de la Terre, montrer que l’énergie mécanique Em du satellite est liée à son énergie cinétique Ec par : Em = - Ec. On note r =RT+h avec h : altitude du satellite. Em= -GMTm/r + ½mv2. de plus v2 = GMT/r d'où : Em= -GMTm/r + ½GMTm/r = -½GMTm/r = -Ec. Si l’on tient à présent compte de la force de frottement de l’atmosphère sur le satellite, en déduire, en le justifiant, son effet sur la vitesse du satellite. L'énergie mécanique du satellite diminue sous l'effet des frottements. Or Em = -Ec : l'énergie
cinétique du satellite augmente ; la vitesse du
satellite croît.
Pour un satellite de masse m en mouvement (quelconque) autour de la Terre, et uniquement soumis à la force gravitationnelle terrestre, l’énergie mécanique peut s’écrire de la même façon que celle d’un point matériel en mouvement rectiligne placé dans un potentiel effectif Ueff(r) dont la courbe représentative est donnée : E= ½m(dr/dt)2+Ueff(r) avec r la distance du satellite au centre de la Terre.
Le satellite est soumis à la force de gravitation conservative exercée par la terre : l'énergie mécanique est donc constante.
position (1) : E <Ueff(r) ce qui impliquerait ½m(dr/dt)2 : c'est impossible. position (2) : état lié : mouvement circulaire uniforme. position (3) : état lié : la trajectoire est une ellipse. position (4) : état libre : la trajectoire est une parabole. position (5) : état libre : la trajectoire est une hyperbole. |
|||||||
|
|
|||||||
|
|