Etude d'un ressort dans deux référentiels ; forces d'inertie ; énergie potentielle effective Mines 2002, ITPE 2011 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

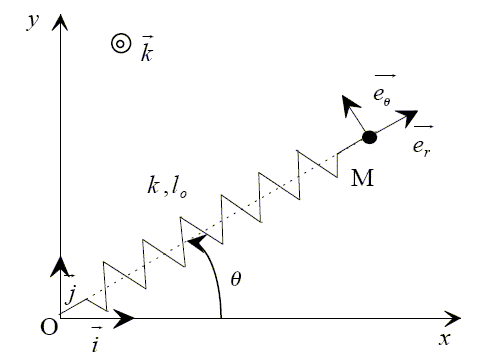
Etude dans le référentiel R du laboratoire. Les vecteurs sont écrits en gras et en bleu. Le mouvement est étudié dans le référentiel du laboratoire assimilé à un référentiel galiléen et associé à un repère (O, i, j, k). Un palet M de masse m peut se mouvoir sans frottement dans le plan ( , O x,y) horizontal (table à coussin d'air par exemple). Le champ de pesanteur est suivant la verticale Oz : g=-gk. La masse m est accrochée à l'extrémité d'un ressort (point M ) de longueur à vide l0 , de raideur k , dont l'autre extremité est fixée en O. La position de M est repèrée dans la base (i, j) par OM = xi +y j ou dans la base (er , eq) par OM = r er. Faire un bilan des forces. Montrer qu'il y a conservation du moment cinétique, LO par rapport à O. Le palet est soumis à son poids ( verticale, vers le bas, valeur mg), à l'action du plan ( verticale, vers le haut, opposée au poids) et à la tension T du ressort ( dirigée suivant OM, valeur k|l-l0| ) . Le moment cinétique LO est donc constant.  A t=0, la masse est lâchée, sans vitesse initiale d'une longueur l=1,2l0 : OM (t=0) =1,2l0 i. Calculer LO. Quelle est la nature de la trajectoire ? LO = mv0^ OM (t=0) ; or v0 est nulle , donc LO est nul. La trajectoire est l'axe Ox. Déterminer l'évolution temporelle de la longueur du ressort, l(t) =OM(t). Préciser l'intervalle de variation de l , longueur du ressort. La seconde loi de Newton s'écrit : T = ma ; -k(l-l0) i = ma ; projection sur l'axe Ox : -k(l-l0) = mx"" et en posant x = (l-l0) : kx+mx"=0 x" + w02 x=0 avec w02 = k/m. Solution générale de cette équation différentielle x(t) =A cos (w0t+j) à t=0 x(0) = 0,2 l0 = Acos j d'où : A = 0,2 l0 et j =0. x(t) =0,2 l0 cos (w0t) ; l = l0 +0,2 l0 cos (w0t). La longueur du ressort varie entre 0,8 l0 et 1,2 l0. On lance la particule d'un point OM0=OM(t=0) =l1 i, avec une vitesse initiale v0 =l1w j. Dans la suite, on travaillera en coordonnées polaires dans le plan (O, x, y). Préciser L0 en fonction de r et dq/dt puis en fonction des conditions initiales et des vecteurs de base. On notera L, le module de L0. LO = mv0^ OM (t=0) = mdq/dt eq^rer = ml1w j ^l1 i =ml12wk. 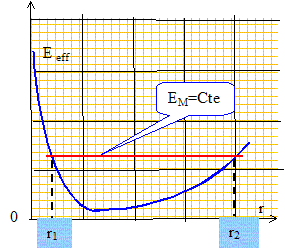Rappeler l'expression de l'énergie potentielle élastique. Ep =½k(l-l0)2 =½k(r-l0)2 Doit-on tenir compte de l'énergie potentielle de pesanteur pour étudier le mouvement ? Non, le mouvement s'effectue dans un plan horizontal. Montrer qu'il y a conservation de l'énergie mécanique EM. Le poids et l'action du support, perpendiculaires à la vitesse, ne travaillent pas. La tension dérive d'une énergie potentielle, c'est une force conservative. L'énergie mécanique est donc constante. Préciser l'expression de EM en fonction des conditions initiales. énergie potentielle élastique initiale : Ep(0) = ½k(l1-l0)2 énergie cinétique initiale : Ec(0) =½m(l1w)2. énergie mécanique initiale EM(0) = ½k(l1-l0)2 + ½m(l1w)2. Préciser l'expression de EM en fonction de r, dr/dt, dq/dt, m , k et l0. valeur de la vitesse à la date t : v = [ (dr/dt)2 + r2(dq/dt)2 ]½. EM= ½k(r-l0)2 + ½m[ (dr/dt)2 + r2(dq/dt)2 ]. Montrer que l'énergie mécanique peut s'écrire EM= ½m (dr/dt)2 + Eeff(r). EM= ½m (dr/dt)2 + ½k(r-l0)2 +½m r2(dq/dt)2. On pose Eeff (r) = ½k(r-l0)2 +½m r2(dq/dt)2= Eeff (r) = ½k(r-l0)2 +½m r2w2. Conservation du moment cinétique : L =ml12w = m r2dq/dt ; dq/dt =l12w /r2 d'où Eeff (r) = ½k(r-l0)2 +½ml14w2 /r2. Tracer l'allure de Eeff (r). La masse peut-elle s'éloigner indéfiniment du pôle d'attraction ? La trajectoire de la particule d'énergie mécanique EM est limitée par les deux valeurs r1 et r2 : la particule est liée au pôle d'attraction et ne peut pas être libre de s'en éloigner indéfiniment. La vitesse de la particule peut-elle s'annuler au cours de son mouvement ? LO = mv^ OM (t) = ml12wk. Le moment cinétique reste constant : en conséquence la vitesse ne peut pas s'annuler. La particule peut-elle passer par le centre d'attraction au cours de son mouvement ? Le moment cinétique reste constant : en conséquence OM=r ne peut pas s'annuler. On cherche à déterminer une condition entre l1 et w pour avoir un mouvement circulaire. Montrer que dans ce cas le mouvement est uniforme. Dans ce cas r = l1 = Cte ; de plus le moment cinétique reste constant : LO = m v^ OM (t) = ml12wk. m v^ OM (t) = m v l1k = ml12wk d'où v = wl1 = Cte. La valeur de la vitesse étant constante, le mouvement est uniforme. Déterminer l1 en fonction de k, l0 et w. Est-elle valable pour tout w ? Lorsque Eeff (r) est minimale, le mouvement est circulaire uniforme de rayon r = l1. dEeff (r) /dr = 0 ; Eeff (r) /dr = k (r-l0) -ml14w2 /r3=0 k (l1-l0) -ml14w2 /l13=0 ; k (l1-l0) =ml1w2 ; kl0=l1 (k-mw2) l1=kl0/(k-mw2). Le dénominateur ne peut être négatif ou nul ; donc w doit être inférieur à (k/m)½.   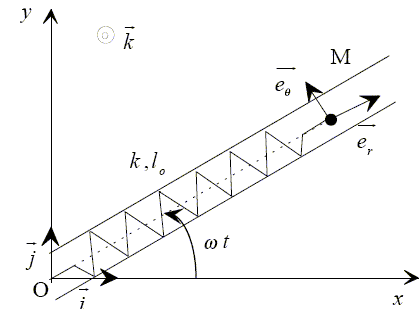Etude dans le référentiel R' en rotation uniforme autour d'un axe fixe. Les vecteurs sont écrits en gras et en bleu. Le mouvement est étudié dans le référentiel R' en rotation uniforme autour d'un axe Oz fixe, de vecteur vitesse W = wk, et associé au repère (O, er, eq, k). On considère une particule M de masse m pouvant se mouvoir sans frottement le long de l'axe (O, er ). Le champ de pesanteur est toujours suivant la verticale Oz : g = -gk. La masse m est accrochée à l'extrémité d'un ressort (point M) de longueur à vide l0, de raideur k, dont l'autre extrémité est fixée en O. La position de M esr repérée dans la base (er, eq) par OM= r er. 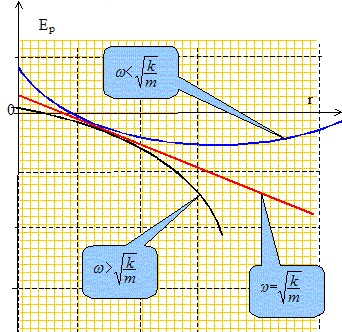Préciser les expressions vectorielles des forces d'inertie dans la base ( er, eq, k). Force d'inertie d'entraînement : fie = mw2 r er. Force d'inertie de Coriolis : fiC = -2mw k ^dr/dt er = -2mw dr/dt eq. Montrer que la force d'inertie d'entraînement dérive d'une énergie potentielle Ep f ie que l'on précisera. Considérons la fonction Ep = -½ mw2 r2. -grad Ep = -dEp/dr er = mw2 r er. La force fie = mw2 r er dérive de l'énergie potentielle Ep = -½ mw2 r2. En est-il de même pour la force d'inertie de Coriolis ou complémentaire ? La force d'inertie de Coriolis est perpendiculaire à la vitesse : elle ne travaille pas et ne dérive donc pas d'une énergie potentielle. Déterminer l'énergie potentielle totale.  Ep = ½k(r-l0)2 -½ mw2 r2. Tracer l'allure de Ep(r). On distinguera trois cas possibles selon la valeur de w.  dEP/dr = k(r-l0)-mw2 r = r(k-mw2 )-kl0. La dérivée s'annule pour r = kl0/ (k-mw2 ). Déterminer la longueur l2 correspondant à la position d'équilibre dans R'. La dérivée s'annule pour r = kl0/ (k-mw2 ) ; la dérivée est positive si r > kl0/ (k-mw2 ) ; la dérivée est négative si r < kl0/ (k-mw2 ) ; Il s'agit donc d'un minimum d'énergie potentielle. l2 = kl0/ (k-mw2 ). A quelle condition sur w le résultat est-il possible ? Cet équilibre est-il stable ? k-mw2 doit êtrte positif soit w < (k/m)½ ; l'équilibre est stable du fait du minimum d'énergie potentielle. Quel est alors le mouvement dans le référentiel du laboratoire ? Circulaire uniforme. Comparer l2 et l1 et conclure. l2=l1 ; dans le cas de ce mouvement circulaire uniforme les deux référentiels sont équivalents.

retour -menu