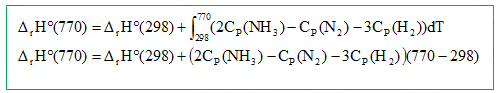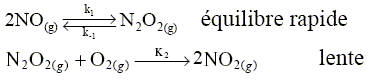Critère d'évolution spontané ; loi de Hess ; enthalpie ; cinétique Mines - Agrégation. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

On ontroduit dans un réacteur 2,00 mol d'acide éthanoïque ( noté A) et 2,00 mol de pentan1-ol ( noté P). On obtient à l'équilibre, à 298 K, sous P= 1 bar, 1,32 mol d'acétate d'amyle ( noté E). On assimilera l'activité d'un constituant à sa fraction molaire globale dans le mélange. Nom de l'ester obtenu, en nomenclature systématique : CH3-COO-CH2-CH2-CH2-CH2-CH3 étanoate de pentyle. Expression et valeur de la constante K de l'équilibre : A + P = E + H2O ; K= aE, éq aH2O, éq / (aA, éq aP, éq) = nE, éq nH2O, éq / (nA, éq nP, éq) avec nE, éq = nH2O, éq =1,32 mol et nA, éq = nP, éq = 2-1,32 = 0,68 mol K= (1,32/0,68)2 = 3,77. 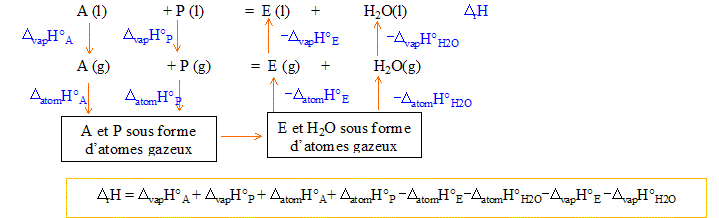Enthalpie standard DrH°de la réaction à 298 K : enthalpie standard DdisH° de dissociation de liaison à 298 K : liaison C-H C-O C=O C-C O-H DdisH° (kJ/mol) 411 358 743 346 460 enthalpie standard DvapH° de vaporisation : corps A P E H2O DvapH° (kJ/mol) 41,6 52,2 43,9 44,0 DatomH°A=3DdisH°(C-H) + DdisH°(C=O) +DdisH°(O-H) +DdisH°(C-O)+DdisH°(C-C) DatomH°P=11DdisH°(C-H) +4DdisH°(C-C) +DdisH°(O-H) +DdisH°(C-O)   DatomH°E=14DdisH°(C-H) +5DdisH°(C-C) +2DdisH°(C-O) + DdisH°(C=O) DatomH°H2O=2DdisH°(O-H) DatomH°A+DatomH°P-DatomH°E-DatomH°H2O=0 kJ/mol DvapH°A+DvapH°P-DvapH°E-DvapH°H2O= 41,6+52,2-43,9-44 = 5,9 kJ/mol DrH° = 5,9 kJ/mol endothermique. en conséquence une élévation de température, à pression constante, déplace l'équilibre dans le sens direct. entropie standard de la réaction à 298 K : enthalpie standard : DrG° = -RT ln H = -8,32*298 ln 3,77 = -3,29 kJ/mol DrG° =DrH° - TDrS° DrS° =(DrH°-DrG°) / T = (5,9+3,29)/298 = 0,0308 kJ mol-1 K-1 = 30,8 J mol-1 K-1. L'équilibre étant réalisé, on ajoute à température et pression constante, 2,00 moles d'acide éthanoïque. Evolution de l'équilibre : quotient initial Qi ( juste avant l'ajout d'acide) : Qi = nE, i nH2O,i / (nA, i nP, i) Qi = 1,32*1,32/ (2,68*0,68) = 0,96 Le quotient initial étant inférieur à la constante d'équilibre, l'équilibre se déplace dans le sens direct. Composition de l'équilibre : avancement (mol) A +P = E +H2O initial 0 2,68 0,68 1,32 1,32 en cours x 2,68-x 0,68-x 1,32+x 1,32+x à l'équilibre xéq 2,68-xéq 0,68-xéq 1,32+xéq 1,32+xéq 0,36 2,32 0,32 1,68 1,68 K= nE, éq nH2O, éq / (nA, éq nP, éq) ; 3,77 = (1,32+xéq)2 / [(2,68-xéq)(0,68-xéq)] 3,77 (2,68-xéq)(0,68-xéq) = (1,32+xéq)2 la résolution donne xéq = 0,36 mol. De l'ammoniac à l'acide nitrique. Industriellement, la synthèse de l'ammoniac se fait selon l'équilibre suivant : N2 + 3H2 = 2NH3. Corps pur Etat Df H° ( kJ/mol ) à 298 K CP ( J mol-1 K-1) H2 gaz 0 28,91 N2 gaz 0 29,63 NH3 gaz -46,210 28,05 Calculer l'enthalpie de réaction, Dr H° ( kJ/mol ) à 298 K. Dr H° =2Df H° ( NH3 ) - 3Df H° ( H2 )-Df H° ( N2 ) Dr H° =2*(-46,210 )= -92,42 kJ/mol. Calculer l'enthalpie de réaction, Dr H° ( kJ/mol ) à 770 K. La réaction est-elle exothermique ou endothermique ? Dr H° ( 770) = -92,42 103 + (2*28,05 - 29,63-3*28,91)* 472= -120,9 kJ/mol. L'enthalpie de réaction étant négative, la réaction est exothermique. L'ammoniac peut ensuite en présence du dioxygène O2 s'oxyder en monoxyde d'azote NO et vapeur d'eau H2O. Ecrire la reaction. 4 NH3 (g) +5 O2 (g) =4 NO(g) + 6 H2O (g). Le monoxyde s'oxyde ensuite selon : 2 NO(g) +O2 (g) = 2NO2(g). En se fondant sur la notion de molécularité, justifier le fait que cette réaction n'ait pas lieu en une seule étape selon 2 NO(g) +O2 (g) = 2NO2(g). Il est très peu probable qu'un choc efficace se produise entre trois molécules. Le mécanisme proposé est le suivant : La vitesse de la réaction est définie par la relation : v =½ d[NO2]/dt où [NO2] est la concentration de NO2. Le mécanisme est-il par stade ou en chaîne ? Justifier. L'intermédiaire N2O2 est consommée à l'étape 2 ; il n'est plus régénéré : donc mécanisme par stades. Calculer la vitesse en fonction de k1, k-1 ,k2 ,[NO] et [O2]. Quel est l'ordre global de la réaction ? L'étape 2 donne : d[NO2]/dt =2k2 [N2O2][O2] d[N2O2]/dt = k1[NO]2-k-1[N2O2]-k2[N2O2][O2] [N2O2] est un intermédiaire très réactif , il réagit au fur et à mesure qu'il se forme : par conséquent d[N2O2]/dt =0. [N2O2] = k1[NO]2 k-1+k2[O2] ~ k1[NO]2 k-1 k2[O2] est négligeable devant k-1, l'étape 1 étant rapide et l'étape 2 lente. Par suite ½d[NO2]/dt = k1k2[NO]2[O2] k-1 L'ordre est égal à 2+1 = 3.

retour -menu