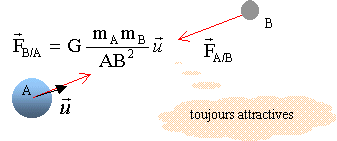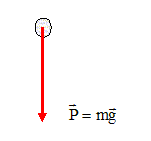Première loi de Newton, vecteur vitesse, référentiel lycée. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

" Newton commence à réfléchir à l'interaction gravitationnelle en 1665 ( il a 23 ans) : à cette époque, les scientifiques croient à l'existence de tourbillon célestes pour expliquer l'univers. Pour Descartes, le soleil et les planètes baignent dans une matière fluide ; le mouvement perpétuel des planètes autour du soleil s'explique par de gigantesques tourbillons engendrés par l'impulsion initiale reçue par les planètes ; ce sont les forces de contact entre le fluide et les planètes qui justifient le mouvement. Pendant plus de 20 ans Newton s'interroge et abandonne progressivement le modèle des tourbillons célestes ; il compare l'effet de la force qui relie la lune sur son orbite avec celle que subit un corps en chute libre sur la terre ". Comment Descartes justifiait-il le mouvement des planètes ? "le mouvement perpétuel des planètes autour du soleil s'explique par de gigantesques tourbillons célestes " Quelle analogie Newton a t-il recherché pour expliquer le mouvement de la lune ? La force exercée par la terre sur la lune est analogue à celle exercée par la terre sur une pomme qui se décroche de l'arbre. Newton montre que le mouvement des objets sur Terre et des corps célestes sont régis par les mêmes lois physiques. Pourquoi Newton a t-il eu raison de faire cette analogie ? En se basant sur les lois de Kepler sur le mouvement des planètes, il expose sa théorie sur la gravitation universelle. Enoncer la loi qui a permis de justifier le mouvement de la lune autour de la terre . - L'interaction gravitationnelle (Newton 1867) entre les masses. Deux corps A et B de masses respectives mA et mB séparés d'une distance AB exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit.  Ces forces sont proportionnelles aux masses et inversement proportionnelles au carée de la distance qui les séparent.   . . 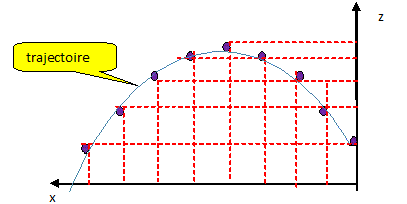Mouvement d'une pierre. On repère les positions du centre d'inertie de la pièrre à intervalle de temps réguliers.   Nature du mouvement suivant l'axe horizontal : Les droites verticales sont pratiquement équidistantes : les distances, suivant Ox, parcourues durant des durées égales, sont donc égales. La composante horizontale de la vitesse est constante : le mouvement est donc uniforme suivant Ox. Nature du mouvement suivant l'axe vertical : Les droites verticales ne sont pas équidistantes : les distances, suivant Oy, parcourues durant des durées égales, sont diférentes. La composante verticale de la vitesse n'est pas constante : le mouvement n'est donc pas uniforme suivant Oy. La composante verticale de la vitesse décroît lors de la montée, s'annule au point le plus haut, puis croît à la descente. Nature de la force exercée sur la pierre si on néglige les frottements : le poids, verticale, vers le bas, valeur P= mg.   Justifions le mouvement de la pierre d'après le principe d'inertie. Dans un référentiel galilléen, un solide pseudo-isolé ( la somme vectorielle des forces est nulle ) est : - soit au repos si la vitesse initiale est nulle - soit son centre de gravité est animé d'un mouvement rectiligne uniforme. Suivant Ox, aucune force n'intervient : le mouvement du cente d'inertie de la bille suivant Ox est donc rectiligne uniforme. Suivant Oy, le poids intervient : le mouvement du cente d'inertie de la bille suivant Oy n'est donc pas rectiligne uniforme. 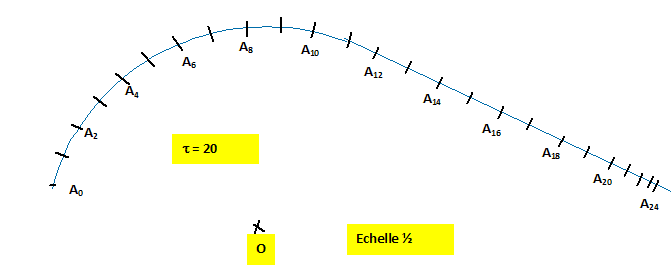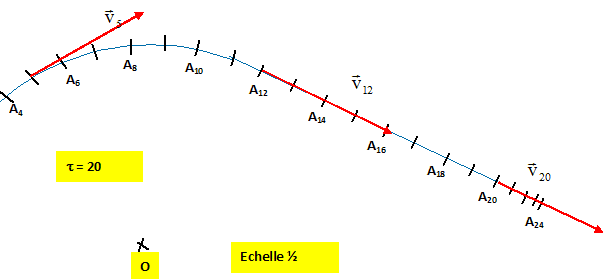Sur une table horizontale, un mobile à cousin d'air est relié au point O par un fil inextensible. Le mobile est lancé et on enregistre les positions de son centre d'inertie à intervalles de temps égaux t = 20 ms. Dans un premier temps le fil est tendu, puis il casse. Enfin dans un troisième temps on supprime le coussin d'air. On distingue 3 phases dans cet enregistrement. Indiquer la nature du mouvement dans chaque phase et justifier. A0A10 : circulaire uniforme : les distances parcourues pendant des temps égaux sont égales. A11A20 : : rectiligne uniforme : les distances parcourues pendant des temps égaux sont égales. Au dela rectiligne déccéléré : les distances parcourues pendant des durées égales diminuent. Calculer le valeur du vecteur vitesse en A5, A12 et A20. Représenter ces vecteurs. Valeur de la vitesse en A5 : mesurer A4A5 + A5A6 ; A4A5 + A5A6 = 2 cm ; doubler pour tenir compte de l'échelle ( exprimer en mètre) : 4 cm = 0,04 m puis diviser par 2 intervalles de temps soit 0,040 s v5= 0,04/0,04 = 1 m/s. Valeur de la vitesse en A12 : même méthode v12= 1 m/s. Valeur de la vitesse en A20 : même méthode v20= 0,8 m/s. Le vecteur vitesse est porté par la tangente à la trajectoire au point considéré et a toujours le sens du mouvement. Echelle : 1 cm pour 0,2 m/s. Dans quel cas le vecteur vitesse est-il constant ? Justifier. Un vecteur est constant si sa direction, son sens et sa valeur restent constants. phase 1 : non, car la direction change ( tangentes en différents points du cercle). phase 2 : oui, direction, sens et valeur constantes. phase 3 : non ( la valeur de la vitesse diminue).  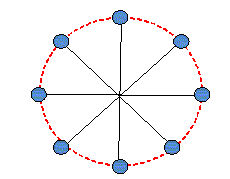Pour comprendre le mouvement de la lune, Newton étudie le mouvement d'une pierre dans une fronde. La pierre est retenue par les brins de la fronde. Dans quel référentiel étudie t-on le mouvement de la pierre ? On choisit un référentiel afin que l'étude du mouvement de la pierre soit le plus simple possible. Référentiel lié à la main, immobile, de la personne qui tiend la fronde, ou encore référentiel lié à la personne immobile ( c'est à dire un référentiel lié à la terre). La longueur des brins de la fronde restant constante, décrire le mouvement de la pierre. La distance de la pierre à la main reste constante ; la pierre décrit un cercle : le mouvement est circulaire. 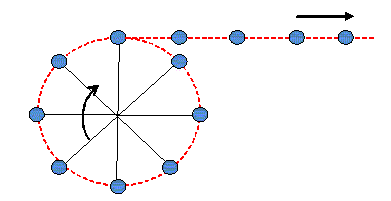Le mouvement de la pierre est filmé ; les durées entre chaque prise de vue (différentes positions de la pierre) sont constantes. Les distances parcourues par la pierre entre deux prises de vue sont constantes : Le mouvement est uniforme : la valeur de la vitesse est constante. Les forces qui agissent sur la pierre se compensent-elles ? Le mouvement n'est pas rectiligne uniforme : dans un référentiel terrestre supposé galiléen, d'après le principe de l'inertie, les forces exercées sur la pierre ne se compensent pas. On lâche un brin de la fronde. Juste après le lâcher, le mouvement de la pierre est-il rectiligne ? uniforme ? Les différentes positions de la pierre sont sur une droite : le mouvement est rectiligne. Le mouvement de la pierre est filmé ; les durées entre chaque prise de vue (différentes positions de la pierre) sont constantes. Les distances parcourues par la pierre entre deux prises de vue sont constantes : Le mouvement est uniforme : la valeur de la vitesse est constante. Exprimer et calculer la vitesse moyenne de la pierre en m/s et en km/h sachant qu'elle parcourt 10 m en 0,3 s. vitesse (m/s) = distance (m) durée (s) = 10 0,3 =33,3 m/s. 1 km = 1000 m ; 1 heure = 3600 s. Passage de la vitesse exprimée en m s-1 au km h-1 : 33,3 *3,6 = 120 km / h. On lâche une goutte d'eau colorée dans une grande éprouvette contenant de l'huile. La chronophotographie de la chute de la goutte est donnée ci-contre. Quel est le référentiel d'étude du mouvement de la goutte ? On choisit un référentiel afin que l'étude du mouvement de la goutte soit le plus simple possible. Référentiel du laboratoire par exemple : ( c'est à dire un référentiel lié à la terre). Décrire les deux phases du mouvement de la goutte. Les 4 premières images : la durée séparant chaque image est la même. Les distances parcourues par la goutte sont croissantes : la vitesse augmente. Mouvement rectiligne accéléré. A partir de la quatrième image, les distances parcourues par la goutte, pendant des durées égales, sont identiques : la valeur de la vitesse est constante. Mouvement rectiligne uniforme. D'après le principe d'inertie, les forces appliquées à la goutte se compensent. Lorsque la goutte passe devant le repère R, on déclenche un chronomètre et on mesure la durée t (s) en fonction de la distance parcourue d( cm). d(cm) 2,0 4,0 6,0 8,0 10,0 t(s) 3,1 6,4 9,5 12,6 15,8 Tracer la courbe d=f(t). Conclure. 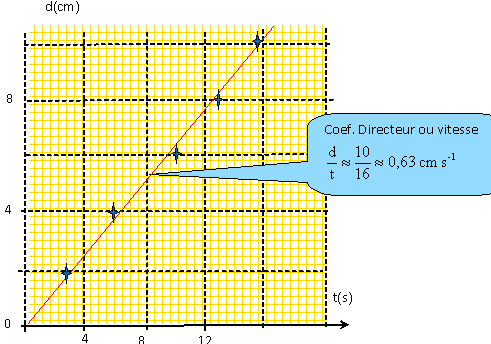La courbe est une droite : les distances parcourues sont proportionnelles aux durées correspondantes. La valeur de la vitesse, coefficient directeur de la droite, est constante. Le mouvement est donc uniforme. La vitesse est proche de 0,63 cm/s.

retour -menu