|
champ électrique crée par un plan infini chargé en surface : condensateur concours ITPE 2008 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
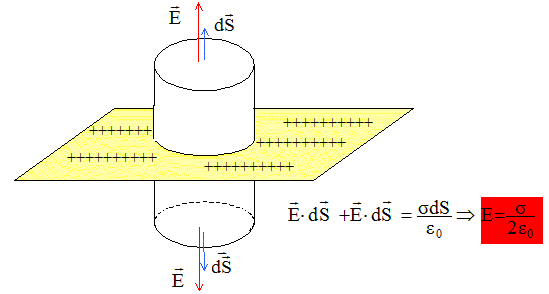
On considère un plan infini xOy portant la densité surfacique de charge s uniforme, situé en z=0. On se place dans un système de coordonnées cartésiennes de sorte que le champ électrique crée par ce plan s'écrive sous la forme E = E(x, y, z). Donner l'unité de s. C m-2 ( charge en coulomb divisée par la surface en m2) Etablir de manière précise par des considérations de symétrie, la direction du champ électrique en un point M. De quelle(s) variable(z) dépend le champ électrique ? Justifier. La distribution de charge est invariante par translation suivant Ox : le champ ne dépend pas de la variable x. La distribution de charge est invariante par translation suivant Oy : le champ ne dépend pas de la variable y. La distribution de charge est invariante par translation suivant Oz : le champ ne dépend pas de la variable z. La distribution de charge est invariante par rotation de l'axe Oz : le champ ne dépend pas de l'angle q. Le champ électrostatique ne dépend pas des variables x, y et z. Tout plan contenant l'axe Oz est plan de symétrie pour la distribution de charge : le champ électrostatique est donc porté par l'axe Oz.
En déduire
E
en tout point de l'espace. Le flux du champ est nul à travers la surface latérale du cylindre, celle-ci étant perpendiculaire au champ.
Le champ subit une discontinuité à la traversée du plan.
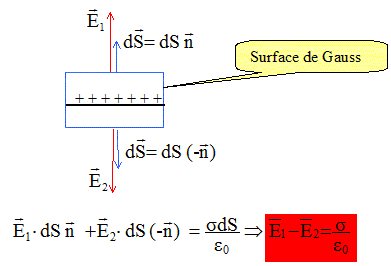
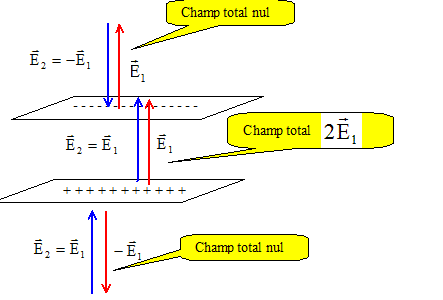
Etude d'un condensateur plan. On considère une deuxième plan infini mobile, parallèle et situé à la distance e du précédent. Ce plan porte une densité surfacique de charge -s uniforme. Les deux plans sont séparés par de l'air dont la permittivité sera prise égale à e0 ( figure 1).
Déterminer le champ électrique total pour z< ; 0< z < e et z > e.
Valeur du champ uniforme entre les armatures E = s/e0. Soit un élément de surface dS de la surface interne de l'armature mobile du condensateur ainsi constitué. Cet élément de surface porte la charge dq. Quelle est la relation entre dq et dS ? dq = -s dS. Déterminer la force électrostatique dF qui agit sur l'élément dS. De quelle nature est cette force ? La charge dq, placée dans le champ de valeur s/(2e0), crée par l'armature positive, est soumise à une force : dF = dq E = -sdSs/(2e0)n = -s2/(2e0) dS n avec n vecteur unitaire de l'axe Oz. En déduire la force totale qui s'exerce sur la surface S de l'armature. F =-s2/(2e0) S n soit en valeur : F = s2/(2e0) S. Montrer que l'on peut définir une pression dite électrostatique qui s'exprime sous la forme p= s2/(2e0). Une force divisée par une surface a la dimension d'une pression p = F/S = s2/(2e0).
On fixe sur l'armature mobile un ressort de constante de raideur k. L'autre extrémité du ressort est fixe. ( figure 2) L'armature mobile peut se translater dans la direction Oz. La position qui correspond au contact entre les armatures est choisie comme origine de l'axe Oz, pour cette position, z=0. On applique une tension réglable U entre les armatures du condensateur. En l'absence de tension ( U=0 V) et à l'équilibre, la distance des armatures est z0. Lorsque U est différent de zéro, la norme de la résultante des forces électrostatiques qui agissent sur l'armature mobile s'écrit : Fe = KU2/z2 où K est une constante positive ( on suppose qu'un système de butée empèche les armatures d'entrer en contact ). On néglige l'action de la pesanteur et on a toujours z >0. Exprimer
Fe. Déterminer l'expression de la force mécanique Fm exercée par le ressort sur l'armature mobile en fonction de k, z0 et z. valeur de Fm : k|z-z0|. Lorsqu'on applique la tension U, déterminer la position d'équilibre de l'armature mobile. Les forces Fe et Fm sont opposées : elles ont même valeur. e0 S U2
/(2z2 )= k|z-z0|. On donne ci-dessous l'allure des courbes représentant les évolutions des normes de Fe et Fm en fonction de z.

Pour chacune des courbes discuter l'existence de position(s) d'équilibre. cas n°3 : Fe est toujours plus grande que Fm : il n'y a pas de position d'équilibre. cas n°2 : Fe est égale à Fm pour une seule valeur de z ; il y a une position d'équilibre. cas n°1 : Fe est égale à Fm pour deux valeurs de z notées z1 et z2 avec z1 < z2 ; il y a deux positions d'équilibre. Par un raisonnement graphique, déterminer la stabilité de(s) position(s) d'équilibre. cas n°2 : si on s'écarte de la position d'équilibre, alors Fe devient supérieure à Fm : l'équilibre est instable. cas n°1 : si on s'écarte de la position d'équilibre, tout en gardant z1 < z <z2 , alors Fm devient supérieure à Fe : l'équilibre est stable. |
|||||||
|
|
|||||||
|
|