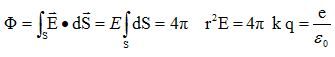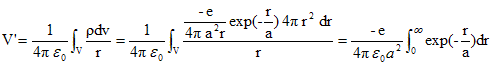Potentiel de Yukawa Concours ITPE 2004. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Les vecteurs sont écrits en gras et en bleu. On considère un point M, un repère fixe d'origine O et on appelle r la distance OM. Une distribution de charges électriques crée en tout point situé à la distance r de O, un potentiel électrostatique : V(r) = k q r exp -r a avec q = e = 1,6 10-19 C, k = 1/(4pe0) = 9 109 S.I; a = 0,1 nm. Déterminer, le champ électrique au point M. Le potentiel ne dépend que de r, la relation E=-grad V s'écrit : E(r) = - dV(r) dr On pose u = 1 r ; v = exp -r a ; u' = -1 r2 ; v' = -1 a exp -r a E(r) = k q r2 exp -r a [ 1+ r a ] Que devient l'expression de ce champ au voisinage de l'origine ?     Au voisinage de l'origine r <<a : exp(-r/a) tend vers 1 et (1+r/a )~ 1 E(r) = k q r2 Il s'agit d'un champ coulombien. Si r >>a, l'exponentielle décroît très vite, le champ E(r) et le potentiel V(r) s'annulent rapidement. "a" caractérise la portée du potentiel et du champ. Calculer le champ pour r= a. a = 10-10 m. E(a)= 9 109 *1,6 10-19 exp(-1) 10-20 [ 1+1] ~ 1,1 1011 V m-1. Le champ électrique ne dépendant que de r, on peut écrire la relation entre le champ et la charge volumique r de la forme : 1 r2 d r2E(r) dr = r e0 Donner l'expression de la charge volumique en tout point de l'espace différent de O. r2E(r) = kq exp -r a [ 1+ r a ] Dériver par rapport à r en posant : v = 1+ r a ; v' = 1 a ; u = exp -r a ; u' = -1 a exp -r a d r2E(r) dr = kq -r a2 exp -r a d r2E(r) r2 dr = kq -1 a2 r exp -r a = r e0 r = = - e0 kq a2 r exp -r a r = = - e 4pa2 r exp -r a A l'aide du théorème de Gauss, calculer la charge placée en O. Le champ E(r) au voisnage de O s'exprime par : E(r) = kq / r2 Calcul du flux F du champ E(r) = kq / r2 à travers la sphère de rayon r, centrée en O. Le champ électrique est radial et sa valeur est constante sur toute la sphère de rayon r. Or le flux du champ électrique sortant d'une surface fermé est égal à la charge intérieur divisée pa e0 : La charge intérieure est positive, ponctuelle, centrée en O de valeur + e. En déduire l'expression du potentiel V créé par cette charge. Potentiel créé par la charge ponctuelle +e à la distance r : V = e 4pe0r + constante Etablir l'expression du potentiel V' créé au point O par la charge répartie dans l'espace, à l'exclusion de l'origine. Calculer ce potentiel. V+V' = k q r exp -r a Calculer l'énergie nécessaire pour amener jusqu'à une distance finie du point O la charge placée en ce point.

retour -menu