|
électricité : étude énergétique d'un conducteur ohmique capes agricole 2004 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On étudie l'échauffement de fils de cuivre nus, de sections circulaires, de différents diamètres, soumis à des courants continus de différentes valeurs. Dans une enceinte isotherme de température q où l'atmosphère est au repos, on dispose rectilignement quatre échantillons des fils à étudier. On envoie dans chacun des fils, un courant continu de valeur croissante. Pour différentes valeurs de l'intensité, lorsque l'équilibre thermique est atteint, on place sur chacun des fils un cristal d'un composé organique dont la température de fusion est qf. On note pour chacun des fils l'intensité pour laquelle la fusion du cristal est observée. Les résultats sont consignés dans le tableau suivant :
Données : Cuivre: - chaleur massique : c = 380 J.K-1.kg-1 ; résistivité : r = 1,67. 10-8 W.m ; masse volumique m = 8960 kg.m-3. Établir l'expression de la température d'équilibre d'un fil (qéq) en fonction des paramètres suivants : la température ambiante q0, la résistivité r du métal constitutif du fil, le diamètre du fil d, l'intensité I du courant qui le parcourt, le coefficient d'échange thermique k entre le fil et le milieu extérieur. (k exprime la proportionnalité de la puissance dissipée avec la surface rayonnante et avec l'écart de température entre le fil et le milieu extérieur). résistance : R = rL/ S avec S = pd2/4 ; R = 4 rL/ (pd2) Puissance joule : PJ= RI2 = 4 rLI2/ (pd2) Surface latérale rayonnante : s =p d L Puissance dissipée par rayonnement : P= k s (qéq-q0). En régime permanent : k s (qéq-q0) = 4 rLI2/ (pd2) k p d L (qéq-q0) = 4 rLI2/ (pd2) ; qéq-q0= 4 rI2/ (kp2d3) qéq=q0+ 4 rI2/ (kp2d3).
Décrire succinctement les paramètres dont dépend le coefficient d'échange thermique k. nature du métal., épaisseur du matériau, phénomène de convexion autour du fil conducteur Calculer sa valeur dans chacun des cas, puis sa valeur moyenne. Commenter ces résultats. k = 4 rI2 / [ p2d3 (qéq-q0) ]. k =4*1,67 10-8/( 3,142*(53-20)) I2 / d3 = 2,05 10-10I2 / d3. k = 0,205 I2 / d3 avec d exprimé en mm.
J (A m-2)= I (A) / section du fil (m2) Calculer sa valeur admissible pour chaque fil de cuivre nu, en sorte que sa température ne dépasse pas qéq = 53 °C.
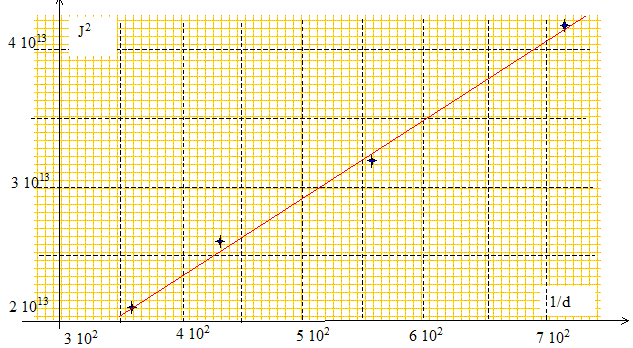
Établir l'expression de la densité de courant admissible pour une température de fonctionnement q donnée, dans un conducteur de section circulaire et de diamètre connu d et de résistivité r. En régime permanent, la puissance reçue par effet joule compensent la puissance perdue par conduction à travers la surface latérale du fil. RI2 = 4r L/(pd2) I2 = kpd L (q-q0). 4I2/(p2d3) = k (q-q0) / r ; or J=4I/(pd2) ; J2=16I2 /(p2d4) J2 d/4 = k (q-q0) / r ; J2 = [4k (q-q0) / r] * 1/d. Confirmer graphiquement les résultats expérimentaux en examinant l'allure de J2 = f(1/d).
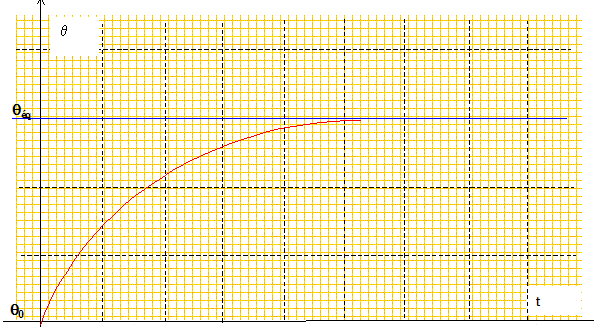
On remplace un conducteur de cuivre monobrin de section circulaire S et de diamètre d1, par un conducteur de cuivre de même section, constitué de n = 16 brins, chacun de section s et de diamètre d2. Déterminer la valeur de l'intensité admissible dans le conducteur multibrins, pour une même température d'équilibre que précédemment. Commenter ce résultat. Résistance du conducteur monobrin : R1=rL/S=4rL/(pd12) Résistance du conducteur multibrins ( 16 conducteurs en dérivation) : R2=rL/(16s) =4rL/(16pd22) R1I12 = 4r L/(pd12) I2 = kpd1 L (q-q0) ; I12 = kp2d13 (q-q0) / (4r) R2I22 = 4r L/(16pd22) I2 = kpd2 L (q-q0) ; I22 = 16 kp2d23 (q-q0) / (4r) I22 / I12 =16[d2/d1]3 Or 16 s= S soit 16pd22=pd12 ; 4d2 =d1 ; d2/d1=1/4 I22 / I12 =16[d2/d1]3 = 4 ; I2 = 2 I1. L'intensité admissible a doublé dans le conducteur multibrins : la puissance admissible doublera également. Étude du régime transitoire. La résistance du fil est supposée indépendante de la température. Déterminer l'expression q(t) de la température d'un fil en fonction du temps, à partir de l'instant t = 0 où le fil à la température initiale q0 est parcouru par un courant continu constant d'intensité I. Bilan énergétique : q, température du fil à la date t ; q +dq, température du fil à la date t+dt. flux thermique de conduction à travers la surface latérale : - kpd L (q-q0). Volume du cuivre : pd2/4 L ; masse de cuivre : pd2/4 mL ; capacité thermique : pd2/4 c mL énergie correspondante : pd2/4 c mL dT ; puissance : pd2/4 c mL dq/dt Puissance reçue par effet Joule : R I2 = 4 rLI2/ (pd2) Bilan : - k pd L (q-q0) + 4 rLI2/ (pd2)= pd2/4 c mL dq/dt ; pd2/4 c m dq/dt + k pd q =k pd q0+ 4 rI2/ (pd2). On pose t = c md / (4k) d'où dq/dt +1/t q =1/t q0+ 4 rI2/ (tp2d3).(1) Solution générale de l'équation sans second membre : q= A exp(-t/t ). solution particulière de (1) correspondant au régime permanent : q = q0+ 4rI2/ (kp2d3). Solution générale de (1) : q = A exp(-t/t )+ q0+ 4rI2/ (kp2d3) A t=0, q = q0 d'où A = - 4rI2/ (kp2d3) q = 4rI2/ (kp2d3) [1-exp(-t/t ) ] +q0. Or qéq=q0+ 4 rI2/ (kp2d3). q =( qéq-q0 )[1-exp(-t/t ) ] +q0.
Représenter qualitativement l'allure de la courbe q(t).
La température d'équilibre recherchée étant qéq = 53 °C, calculer, pour le fil référencé 1, le temps au bout duquel cette température est atteinte à 0,01°C près, sachant que la température ambiante vaut q0 = 20°C. t = c md / (4k) =380*8960*1,4 10-3 /(4*7,47) =160 s. (q -q0 )=( qéq-q0 )[1-exp(-t/t ) ]. 1-(q -q0 ) /( qéq-q0 ) = exp(-t/t ) ; ( qéq-q ) / ( qéq-q0 ) =exp(-t/t ) ln[ ( qéq-q0 ) /( qéq-q )]= t/t ; t =t ln[ ( qéq-q0 ) /( qéq-q )] t = 160 ln(33/0,01) = 1,3
103 s =21
min.
a =1/R dR/dq avec a = 4,27 10-3 S.I. Etablir l'expression de la résistance d'un fil conducteur métallique en fonction de sa température. d (ln R) = a dq ; ln(R/R0) = a( q-q0 ) R = R0 exp[a( q-q0 )]. Une ligne est constituée de 100 m du fil référencé 1. Elle est située dans une ambiance à la température uniforme de 20°C. Calculer la valeur de sa résistance à la température de 20°C. R0 =4rL/(pd2) = 4*1,67 10-8*100 / (3,14*(1,4 10-3)2) ; R0 = 1,08 W. Calculer la valeur de sa résistance lorsqu'elle est parcourue par un courant de 10 A. qéq = 53 °C ; R = 1,08 exp(4,27 10-3*33) ; R = 1,24 W.
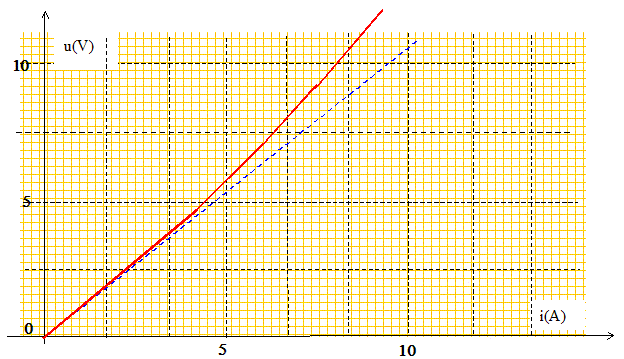
Tracer l'allure de la caractéristique u = f(i) de cette ligne sur un graphe à une échelle judicieusement choisie.
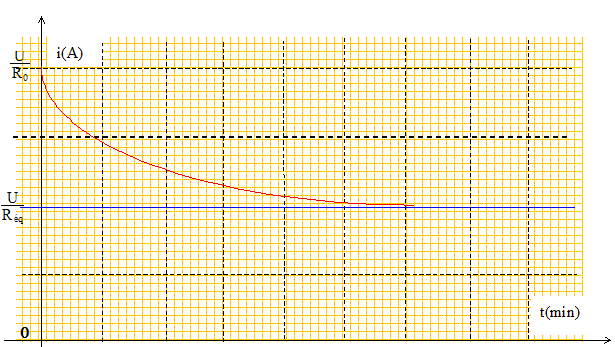
Par inadvertance, on branche un générateur de tension continue de 12 V aux bornes de cette ligne. Donner l'allure du courant i = f(t) qui la traverse, telle que l'on pourrait l'observer avec un oscilloscope à mémoire judicieusement branché. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|