|
Lentilles de Fresnel : anneaux dioptriques ; catadioptres concours Capes interne 2008 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
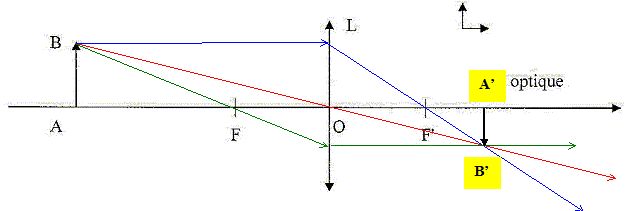
Les systèmes optiques possèdent en général un axe de symétrie appelé axe optique. Soit un point A de cet axe envoyant un faisceau sur l'instrument : à la sortie si le faisceau converge en un point A' situé sur l'axe, on dit que A et A' sont conjugués. Stigmatisme rigoureux pour un couple de points A et A' conjugués : tous les rayons issus de A passent par A'. Un miroir plan est rigoureusement stigmatique pour tous couples de points (A, A'). Aplanétisme : le stigmatisme doit être rigoureux pour le couple A et A' et le couple B et B' ; B et B' se trouvant dans un plan de front. Conditions de Gauss : l'objet doit être de petites dimensions et placé au voisinage de l'axe optique principal du système optique. On élimine ainsi les rayons lumineux trop inclinés sur l'axe optique. Construire l'image A'B' d'un objet AB donnée par une lentille mince. Compléter le schéma ci-dessous.
Définir le grandissement et établir la formule de conjugaison. Les distances algébriques sont écrites en gras et en bleu. Dans les triangles semblables OAB et OA'B' : :
OA' /
OA =
A'B' /
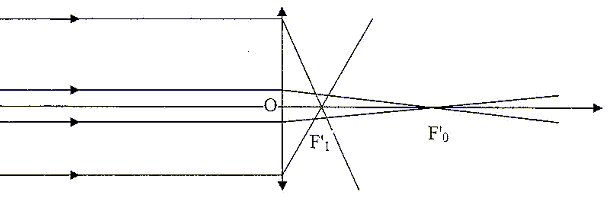
AB. or OH = AB : F'A' /F'O =AB' /A'B = OA'/OA. Or F'A' =F'O +OA' d'où 1 +OA' /F'O =OA'/OA. 1/OA' +1/F'O = 1/OA ; 1/OF' =1/OA' - 1/OA. L'expérience montre que hors conditions de Gauss, une lentille mince n'est plus stigmatique. Un faisceau incident de lumière parallèle ne focalise pas au fyer image F' de la lentille. Les rayons périphériques focalisent plus près du centre optique (F'1 ) que les rayons qui respectent les conditions de Gauss qui focalisent en (F'0 ) :
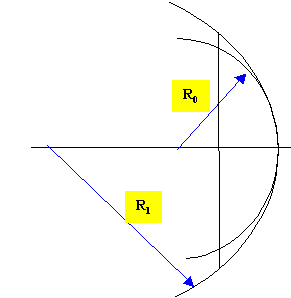
Que peut-on dire de R1 par rapport à R0 ? Augmenter le rayon R, c'est faire décroître la vergence, donc augmenter la distance focale. Si R1 est supérieur à R0, F'1 se rapproche de F'0. Supposons que nous tronquions toute la périphérie de la lentille mince non stigmatique, et que nous rajoutions cette seconde lentille de rayon R1, quelle serait l'allure de cette lentille ?
Le faisceau émis par cette lentille stigmatique sera parallèle à l'axe optique si une source ponctuelle est placée au foyer F.
Lentille de Fresnel.
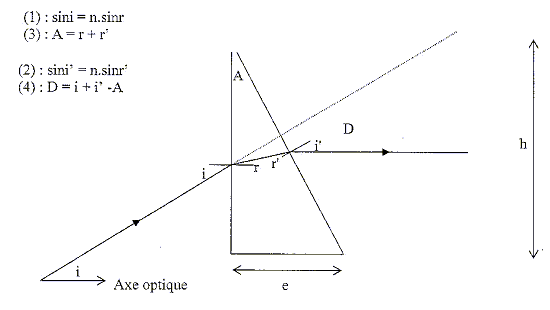
On modélise chaque anneau dioptrique par un prisme d'indice n et d'angle au sommet A. Soit un rayon lumineux arrivant sous un angle d'incidence i sur l'un des prismes de la lentille, on appelle D sa déviation. Justifier les 4 relations données ci-dessous :
dioptre d'entrée nair = 1 : la loi de Descartes pour la réflexion s'écrit : nair sin i = n sin r soit sin i = n sin r. diopre de sortie :la loi de Descartes pour la réflexion s'écrit : n sin r' = nair sin i' soit sin i' = n sin r'.
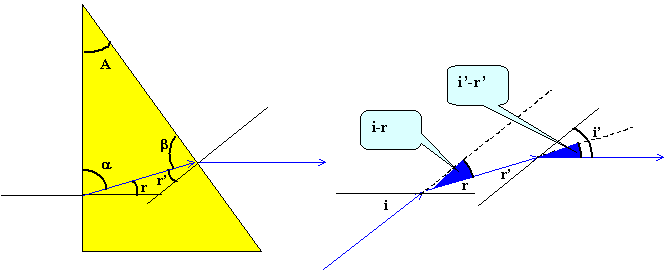
angle a + b supplément de A ; a + r =90 ; b +r'=90 ; a + b = 180-A ; d'où A = r+r'. Déviation sur le dioptre d'entrée : i-r ; déviation sur le dioptre de sortie : i'-r' déviation totale : D= i-r+i'-r' = i+i'-A.
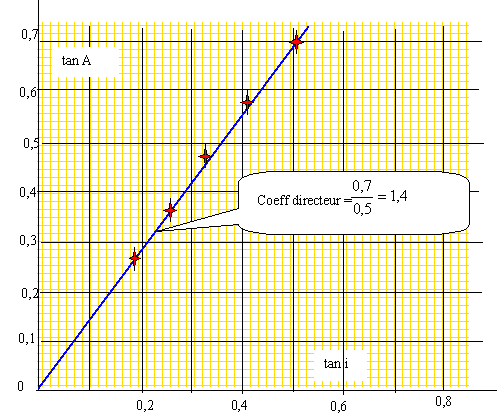
On souhaite que le rayon émergent soit parallèle à l'axe optique de la lentille. Quelle relation existe t-il entre D et i ? Les angles D et i sont égaux. Exprimer sin i en fonction de A et n. D=i+i'-A = i soit : i'= A ; sin A = n sin r' ; r' =arcsin[sin A / n] ; r =arcsin[sin i / n] r+r'=A = arcsin[sin i / n] + arcsin[sin A / n] sin i =n sin[A-arcsin[sin A / n]. Compléter le tableau : n=1,7.
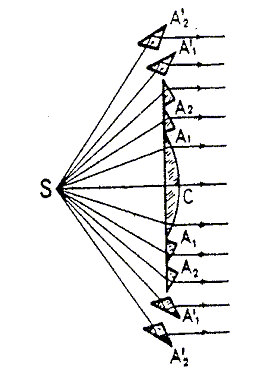
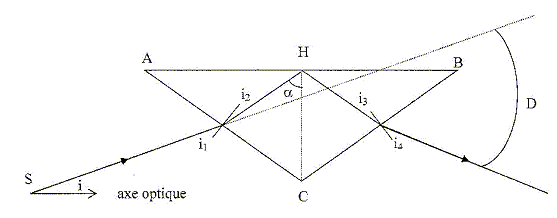
Sachant que toutes les bases des prismes ont la même longueur e ( largeur du centre de la lentille), on appelle h la hauteur du prisme. Exprimer h en fonction de b et tan i. tan A = e/h ; h = e/tan A ; et tan A = b tan i d'où : h = e/ (b tan i ). Si e = 10 cm, i = 15° sur le premier disque, calculer A1 et h1. h1 =10/(1,4 tan 15) =26,6 soit 27 cm. A1 = arctan(e/h) = arctan(10/26,6) =20,6 soit 20 °. Comment varie A et h quand i augmente ? Quand i augmente , tan i augmente et h diminue. Si h diminue, e/h augmente et A augmente. Anneau catadioptrique. Une lentille de Fresnel est constituée de 5 à 6 anneaux dioptriques et de 10 à 15 anneaux catadioptriques pour des angles supérieuurs à 35 °. Les anneaux catadioptriques sont modélisés par des prismes dont la base ABC est constituée d'un triangle isocèle d'angle au sommet égal à 110°. Considérons l'un de ces prismes pour lequel AB est parallèle à l'axe optique de la lentille, placé dans l'air ; n= 1,7.
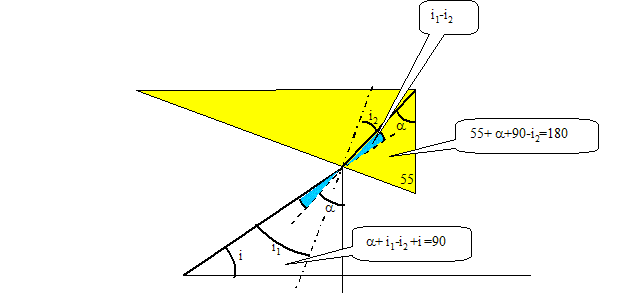
Déterminer l'expression de l'angle limite, noté aL en H, point d'incidence du rayon AB. en H : nverre sin a = nair sin r. A la limite de la réflexion totale : r = 90° ; sin aL =1/nverre = 1/1,7 =0,588 ; aL =36°. A quelle condition sur a y a t-il réflexion totale en H ? si a >aL il y a réflexion totale en H. La déviation imposée par le prisme peut s'écrire : D = p-2a-[(i1-i2)+ (i4-i3)]. Justifier. Déviation lors de la réfraction sur le dioptre d'entrée : (i1-i2), sens trigonométrique direct Déviation lors de la réfraction sur le dioptre de sortie : (i4-i3), sens trigonométrique direct Déviation lors de la réflexion totale en H : p-2a, sens trigonométrique inverse. D est la déviation dans le sens trigonométrique inverse.
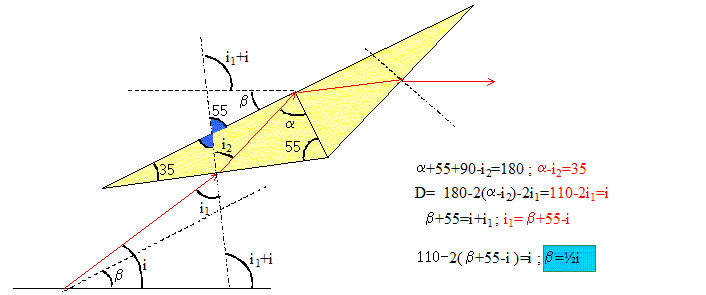
On prendra AH=AB/2. Quelle relation existe t-il entre i1 et i4 ? Entre i2 et i3 ? Par raison de symétrie : i1 et i4 ont même valeur, mais sont de sens contraire ; i2 et i3 ont même valeur, mais sont de sens contraire . Soit i l'angle d'incidence du rayon par rapport à l'axe optique de la lentille de Fresnel, à quelle condition le rayon émergent est-il parallèle à l'axe optique ? L'angle D et i ont la même valeur, mais sont de sens contraire. Déterminer i et commenter cette valeur compte tenu du fait que i doit être supérieur à 35°. D = p-2a-[(i1-i2)+ (i4-i3)] =i ; de plus i1-i2 = i4-i3( déviation dans le sens direct). d'où : a-i2 = 35 ; i1+ i = 55 ; i1-i2 +a+ i =90 ; i1-i2 = 90-i-a. Par suite D = p-2a- 2 (90-i-a) = 2i . Or le rayon émergent est parallèle à l'axe optique si D=i : 2i = i entraîne i=0, contraire au fait que i doit être supérieur à 36°. Si i = 40°, dans quel sens
et de quelle valeur faut-il tourner le prisme dans le plan
pour que le rayon émergent soit parallèle
à l'axe optique
?
La portée d'un phare est limitée par la rotondité de la terre. Déterminer la portée maximale D d'un phare de hauteur H. H = 60,3 m. R= 6380 km. D2 = (R+H)2-R2 = (2R+H)H voisin de 2Rh = 2*6380*60,3 10-3 = 769,4 km2 ; D = 27,7 km. La portée d'un phare est également limitée par l'absorption atmosphérique. Justifier l'utilisation des feux blancs ou rouges ( mais pas bleus) pour les feux de grandes portée. L'atmosphère diffuse plus le bleu que le rouge. |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|