Mécanique des fluides BTS travaux publics 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

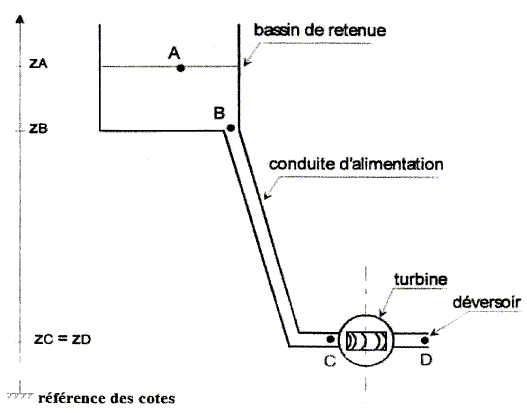
Une turbine est alimentée par une retenue d'eau selon le schéma ci-dessous : Données : - diamètre d de la conduite d'alimentation et du déversoir de section circulaire : d = 0,7 m - pressions aux points A, C et D : pA = pD = 1,01 bar ; pC = 1,10 bar - cote des points A, B et C par rapport à une origine de référence : zA =363 m ; zB=361 m ; zC= 353 m - masse volumique de l'eau r=1,00 103 kg m-3 - intensité de la pesanteur g = 9,81 m s-2. 1 bar = 105 Pa. l'eau sera considérée comme un fluide parfait incompressible. On supposera que le niveau de l'eau dans la retenue est constant. On admettra que les vitesses en C et en D de l'eau sont équivalentes. On rappelle la relation de Bernoulli entre deux sections d'écoulement d'un tube de courant : ½r (v12-v22) +rg(z1-z2) +p1-p2 = Pext QV dans laquelle Pext est la puissance de l'appareil hydraulique. Quelles sont les différentes unités des grandeurs intervenant dans cette relation ? pression p pascal vitesse du fluide v m s-1. masse volumique r kg m-3 altitude z mètre puissance Pext watt (W) débit volumique QV m3 s-1. Calculer la vitesse d'écoulement vC du fluide au point C. Appliquer la relation de bernoulli entre A et C avec vA=0 (le niveau de l'eau dans la retenue est constant) ; entre A et C il n'y a pas de machine donc Pext=0  A correspond à l'état 1 et C à l'état 2 : ½r (0-vC2) +rg(zA-zC) +pA-pC =0 ½r vC2 = rg(zA-zC) +pA-pC vC2 = 2g(zA-zC) + 2(pA-pC) r vC2 = 2*9,81*10 + 2(1,01-1,10) 105 1000 =178,2 Prendre la racine carrée : VC = 13,35 ~13,3 m/s. En déduire le débit volumique QV de l'eau dans la conduite. Il y a conservation du débit volumique ; on fait le calcul en C : QV = VC *0,25 p d2 = 13,35 *0,25*3,14*0,72 =5,135 ~ 5,14 m3 s-1. Justifier que les vitesses d'écoulement en B et C sont égales. Entre B et C il y a conservation du débit volumique ; aux points B et C la conduite à la même section. QV = VC *0,25 p d2 = VB *0,25 p d2 d'où VC = VB. Calculer la pression pB à l'entrée de la conduite en utilisant la relation de Bernoulli entre B et C. VB = VC, le premier terme de la relation sera nul ; entre A et C il n'y a pas de machine donc Pext=0.  B correspond à l'état 1 et C à l'état 2 : +rg(zB-zC) +pB-pC =0 pB =pC -rg(zB-zC) = 1,10 105 -1000*9,81*8 =3,15 104 Pa Calculer la puissance fournie par l'eau à la turbine. Appliquer la relation de bernoulli entre C et D ;  C correspond à l'état 1 et D à l'état 2 ; zC=zD ( le second terme de la relation de Bernoulli est nul) Les vitesses en C et D étant équivalentes, le premier terme de la relation de Bernoulli est nul. Par suite : pC-pD = Pext QV d'où : Pext =QV(pC-pD) Pext = 5,14*(1,10-1,01) 105 = 46,3 kW.

retour -menu