Moteur à courant continu ; moteur asynchrone bac STI génie électrotechnique 2008.

. .

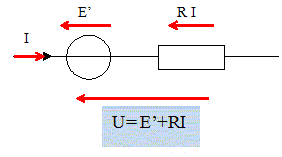
Partie B : moteur à courant continu. La pompe est entraînée par un moteur à courant continu à aimants permanents. La plaque signalétique du moteur indique : 48 V ; 3000 tr/min ; 550 W. Les pertes mécaniques et magnétiques du moteur sont négligeables. Les batteries d'accumulateurs délivrent une tension constante de valeur EB=48 V. Lors du fonctionnement de la pompe, on a mesuré l'intensité du courant dans le moteur : I= 13,7 A. Déterminer le moment Tu du couple utile du moteur. Tu= Pu / W avec Pu = 550 W et W = 2pn/60 = 6,28*3000/60 = 314 rad/s. Tu = 550/314 =1,75 N m. Déterminer la puissance Pa absorbée par le moteur. Pa = UI = 48*13,7 =657,6 W. Déterminer le rendement h du moteur. h =Pu /Pa =550/657,6=0,836 ( 83,6 %)   Déterminer les pertes par effet Joule dans l'induit du moteur et en déduire la résistance R. Les pertes mécaniques et magnétiques du moteur sont négligeables. PJ= Pa-Pu = 657,6-550 =107,6 J. PJ= RI2 ; r= PJ/I2 = 107,6/13,72 =0,57 W. Représenter le schéma du modèle équivalent de Thévenin de l'induit du moteur. Flècher les différentes tensions et intensité. Ecrire la relation entre les différentes tensions. Montrer que la relation entre la force électromotrice E' et la fréquence de rotation n peut s'écrire E' =kn où k est une constante. Calculer la valeur de k en précisant son unité. Aux bornes d'une bobine en mouvement dans un champ magnétique, une fem E' apparaît telle que E'= KFW avec K une constante, F flux maximum à travers les spires et W vitesse de rotation en radian/s. De plus W = 2pn/60 d'où E' = KF2pn/60 = 2pKF /60 n Si le flux est constant E'=k n avec k = 2pKF /60. E'= U-RI = 48-0,57*13,7 = 40 V ; n= 3000 tr/min k = E'/n = 40/3000 = 1,34 10-2 V min tr-1= 0,127 V s rad-1. Déterminer en justifiant, l'intensité Id du courant de démarrage du moteur sous la tension nominale et comparer à I ( 13,7 A). Au démarrage E' est nulle ( n = 0 : pas de puissance mécanique mise en jeu) U= RId ; Id = U/R = 48/ 0,57 = 84 A valeur 6 fois plus grande que le courant nominal I. 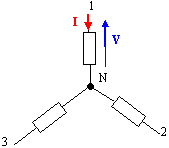Partie D : moteur asynchrone triphasé. Le variateur de vitesse associé au moteur permet de l'alimenter en triphasé avec une fréquence f réglable. Le fonctionnement est dit à U/f constant. La plaque signalétique du moteur porte les indications suivantes : 230V / 400 V ; 50 Hz ; 5,54 A / 3,20 A ; 1430 tr/min ; 1500 W ; facteur de puissance fP=0,84. Pour f=50 Hz, la valeur efficace de la tension entre phase du variateur vaut 230 V. Déterminer en le justifiant le couplage du moteur. La tension aux bornes de chaque bobine du moteur doit être égale à la tension simple 230 V : donc montage étoile. Etude du moteur, alimenté sous 50 Hz, au point de fonctionnement nominal. Déterminer le nombre p de pôles du moteur et la fréquence de synchronisme ns. n = 1430 / 60 ~ 24 tr/s ; ns est légérement supérieur à 24 tout en étant un sous multiple de la fréquence 50 Hz. Donc p= 2 paires de pôles et ns = f/p = 50 /2 ; ns = 25 tr/s ou 1500 tours / minute. Déterminer le glissement g du moteur. g = (ns-n)/ ns = (1500-1430) / 1500 ; g = 0,047. Déterminer la puissance Pa absorbée. Pa = U I 3½ cos j = 400 *3,2*1,732*0,84 ; Pa = 1862 W. 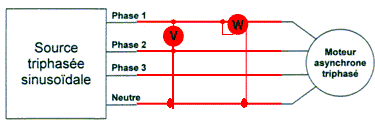Déterminer le rendement h du moteur. h = Pu/Pa =1500/1862 =0,81 ( 81 %) Déterminer le moment Tu du couple utile nominal du moteur. Tu = Pu/ W avec W = 2pn/60 = 2*3,14*1430/60 =149,7 rad/s. Tu = 1500/149,7 = 10 N m. Proposer un schéma de montage permettant de mesurer la puissance reçue par le moteur. Le wattmètre mesure Pa/3 ~ 1862/3 = 620 W. 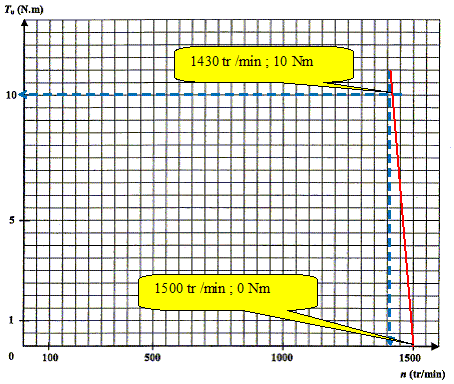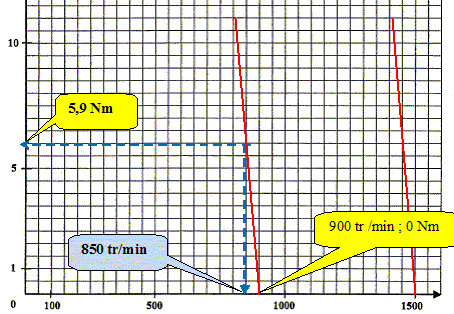Pour f = 50 Hz, tracer sur la figure donnée, la partie utile de la caractéristique Tu(n) en considérant qu'il s'agit d'un segment de droite. Etude du fonctionnement à fréquence réglable. Le moteur étant alimenté à U/f constant, lorsqu'on fait varier la fréquence f, les parties utiles des caractéristiques Tu(n) sont des segments de droites parallèles. La charge entraînée par le moteur présente un couple résistant de moment Tr constant de valeur 10 N m. Tracer la caractéristique Tr(n) sur la figure. Tracer une droite horizontale pasant par T = 10 Nm. Pour une fréquence f= 30 Hz, calculer la fréquence de synchronisme du moteur. si f = 50 Hz : ns = 1500 tr/min ; pour f = 30 Hz : ns = 1500*30/50 = 900 tr/min. Tracer la caractéristique Tu(n) sur la figure et déterminer la fréquence de rotation du groupe moteur-charge. W= 900/60*6,28 =94,2 rad/s ; Tu(900) = 1500 /94,2 = 15,9 N m. Tu-Tr = 15,9-10 = 5,9 N m. 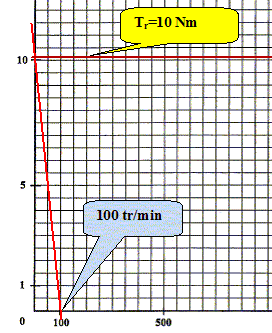Pour que le moteur démarre en entraînant la charge, comparer Tu et Tr lors du démarrage. Tu doit être légerement supérieur à Tr. Déterminer la fréquence minimale de la tension d'alimentation permettant le démarrage du groupe moteur charge. En déduire la valeur efficace de la tension de démarrage. ns =100 tr/min = 100/60 =1,67 tr/s ; de plus ns = f/p : f = p ns = 2*1,67 =3,33 Hz. f/U = constante : f/U= 50/220 = 0,227 ; U = f/0,227 = 3,33 / 0,227 =14,7 V.

retour -menu