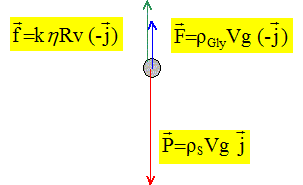Chute d'une bille dans la glycérine : Euler bac S Antilles 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

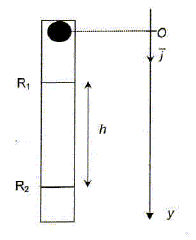
Mesure de la viscosité de la glycérine. La viscosité désigne la capacité d'un fluide à s'écouler. Elle dépend fortement de la température. Un long tube en verre, fermé aux deux extrémités, contient du glycérol de viscosité h et une bille en acier. Le tube est retourné à l'instant t=0, la bille se trouve alors en haut du tube, sans vitesse initiale puis elle tombe verticalement dans le glycérol. La durée de chute Dt' correspond à une distance de chute h connue et mesurée à l'aide de deux capteurs reliés à un chronomètre électronique. Les deux capteurs sont repérés par les positions R1 et R2. g= 9,81 m s-2 ; h= 40,0 cm. Deux traits horizontaux ont été tracés en D et F. Masse volumique de l'acier rS=7,80 103 kg m-3. Rayon de la bille : R= 5,00 10-3 m ; volume de la bille V. Masse volumique du glycérol rgly=1,26 103 kg m-3. La viscosité h s'exprime en Pa.s L'étude est effectuée dans le référentiel du laboratoire supposé galiléen. La bille totalement immergée dans le liquide est lâchée en O sans vitesse initiale. Les vecteurs sont écrits en gras et en bleu. Les forces. Donner l'expression vectorielle du poids P en fonction de rS, V, g et j. Valeur du poids : P= mg avec masse(kg) = volume (m3) * masse volumique ( kg m-3) ; m= VrS. Donner l'expression vectorielle de la poussée d'Archimède F en fonction de rgly, V, g et j. Poids du volume de glycérol déplacé, verticale, vers le haut.    L'intensité de la force de frottement, a pour expression f = khRv ; v est la valeur de la vitesse de chute de la bille, k = 6 p est une constante sans dimension. Donner l'expression vectorielle de la force de frottement f.  Verticale, vers le haut. Représenter ces forces sur un schéma sans souci d'échelle.     Au cours de la chute, la bille atteint très rapidement sa vitesse limite, notée vlim. Lorsque la bille passe devant le trait D( repère R1) et au delà, sa vitesse est constante. 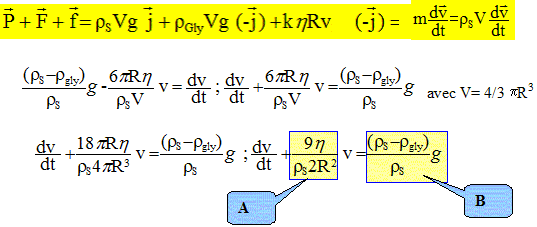Quel est le mouvement de la bille entre les deux repères R1 et R2. Justifier. La vitesse limite a une valeur constante ; de plus le mouvement est rectiligne.  Le mouvement de la bille est rectiligne uniforme. Ecrire la relation vectorielle entre les forces s'exerçant sur la bille lorsqu'elle se trouve entre les deux traits D et F. Justifier la réponse. Le mouvement de la bille étant rectiligne uniforme, le principe d'inertie indique que la bille est pseudo-isolée ( la somme vectorielle des forces est nulle).  (1) A la suite d'une analyse dimensionnelle, donner l'unité de h. h=f /( k R v) M L-1 T-1 k est sans dimension ; R est une longueur : [R] =L ; vitesse v : longueur / temps [v]=L T-1. [R v]=L2 T-1. force f équivalent à une masse * accélération équivalent à masse * longueur / temps2 : [f] =M L T-2. Par suite [h]=M L T-2 / (L2 T-1) = M L-1 T-1 (ou M L-1 T-2 T : Pa s) En déduire l'expression de la viscosité du glycérol h = 2R2g(rS-rgly)/ (9 vlim). (1) donne : (rS-rgly)Vg = 6phRvlim ; h = (rS-rgly)Vg / ( 6pRvlim ) Or V= 4/3 p R3 ; V/( 6pR)= 2R2 /9 d'où : h = 2R2g(rS-rgly)/ (9 vlim). Calculer la vlim si h = 0,400 m Dt' = 1,66 s à 20°C vlim = h / Dt' = 0,400 / 1,66 = 0,241 m/s En déduire la valeur expérimentale de la viscosité h de la glycérine à 20 °C.   h = 2R2g(rS-rgly)/ (9 vlim) = 2*(5 10-3)2*9,81 *(7,80-1,26) 103/(9*0,241)= 1,48 Pa s La valeur théorique de la viscosité du glycérol à cette température est hth=1,49 SI. En effectuant un calcul d'écart relatif, comparer la valeur expérimentale à la valeur théorique. (valeur théorique - valeur expérimentale )*100 / moyenne des valeurs = (1,49-1,48)*100 / 1,485 =0,67 %. A 0,67 % près les valeurs sont identiques. Etude du mouvement de la chute de la bille. A l'instant choisi comme origine des dates, la bille est abandonnée sans vitesse initiale au point O. En utilisant la deuxième loi de Newton montrer que l'équation différentielle liant la vitesse de la bille et sa dérivée par rapport au temps est de la forme : dv/dt + Av = B avec A= 34,4 s-1 et B= 8,23 m s-2. Identifier les expressions des termes A et B dans cette équation.   En déduire la valeur de la vitesse limite atteinte par la bille. Est-elle en accord avec la valeur trouvée expérimentalement ?  dvlim/dt = 0 par suite A vlim=B vlim = B/A vlim =8,23 / 34,4 = 0,239 m/s Il y a accord avec la valeur expérimentale 0,241 m/s. A quelle grandeur physique le rapport 1/A correspond-il ? Même question pour B. 1/A s'exprime en seconde : 1/A représente la constante de temps du dispositif. B a la dimenion d'une accélération : B est l'accélération initiale à t=0.    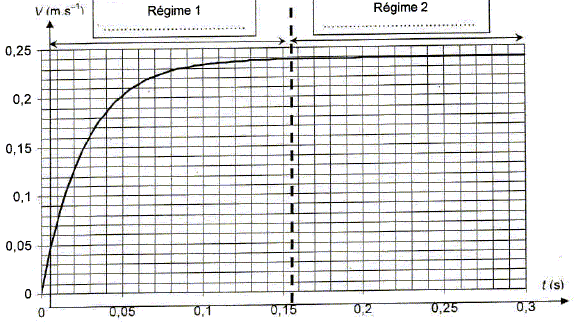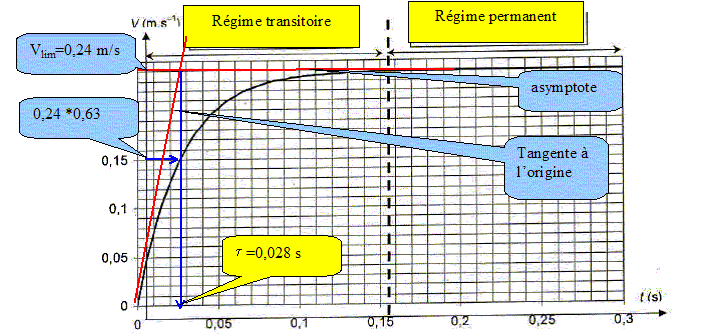On donne la courbe d'évolution de la vitesse au cours du temps. Elle a été obtenue par résolution de l'équation différentielle précédente par la méthode numérique d'Euler. Pour le calcul on a utilisé la relation suivante : v(ti) = v(ti-1)+ a(ti-1) Dt où D t est le pas d'itération du calcul a(ti) = B-A v(ti). On donne un extrait de la feuille de calcul : ti(s) v(m/s) a (m/s2) 0,020 0,127 3,86 0,025 0,146 3,20 0,030 2,65 0,035 0,175 0,040 0,186 1,82 Quel est le pas utilisé pour les calculs ? Dt = 5,0 ms. Calculer la vitesse v6 à la date t=0,030 s et l'accélération a7 à la date t=0,035 s. v(ti) = v(ti-1)+ a(ti-1) Dt v(0,030) = v(0,025)+ a(0,025) * 5 10-3 =0,146 +3,20*5 10-3 = 0,162 m/s. a(ti) = B-A v(ti). a(0,035)= 8,23-34,4 v(0,035) = 8,23-34,4*0,175 =2,21 m/s2. Identifier les deux régimes sur le graphique et déterminer le temps caractéristique t en expliquant votre méthode.

retour -menu